
题目列表(包括答案和解析)
(本小题满分12分)某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组。
(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;
(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;
(3)实验结束后,第一次做实验的职员得到的实验数据为68,70,71,72,74,第二次做实验的职员得到的实验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由。
(本小题满分12分)
山东省某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座概率如下表:
|
|
信息技术 |
生物 |
化学 |
物理 |
数学 |
|
周一 |
|
|
|
|
|
|
周三 |
|
|
|
|
|
|
周五 |
|
|
|
|
|
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为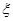 ,求随机变量
,求随机变量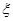 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
求先后被选出的两名技术员中恰有一名女技术员的概率;
请问哪位技术员检验更稳定?并说明理由.
(本小题满分12分)
某中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,
其选报文科理科的情况如下表所示.
| 男 | 女 | |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有
男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有
关? 参考公式和数据:![]()
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
(本小题满分12分)
某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
求先后被选出的两名技术员中恰有一名女技术员的概率;
请问哪位技术员检验更稳定?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com