
题目列表(包括答案和解析)
在研究并行计算的基本算法时,有以下简单模型问题:
用计算机求n个不同的数v1,v2,…vn的和![]() vj=v1+v2+v3+…+vn.计算开始前,n个数存贮在n台由网络连接的计处机中,每台机器存一个数,计算开始后,在一个单位时间内,每台机器至多到一台其他机器中读数据,并与自己原有数相加得到新的数据,各台机器可同时完成上述工作.
vj=v1+v2+v3+…+vn.计算开始前,n个数存贮在n台由网络连接的计处机中,每台机器存一个数,计算开始后,在一个单位时间内,每台机器至多到一台其他机器中读数据,并与自己原有数相加得到新的数据,各台机器可同时完成上述工作.
为了用尽可能少的单位时间使各台机器都得到这n个数据和,需要设计一种读和加的方法,比如n=2时,一个单位时间即可完成计算,方法可用下表表示:
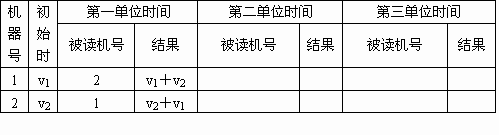
(1)当n=4时,至少需要多少个单位时间可完成计算?把你设计的方法填入下表
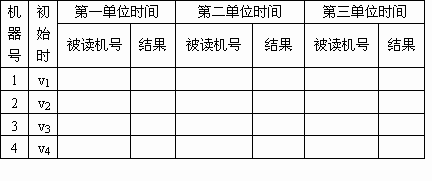
(2)当n=128时,要使所有机器都得到![]() vj,至少需要多少个单位时间可完成计算?(结论不要求证明)
vj,至少需要多少个单位时间可完成计算?(结论不要求证明)
 •
• ,…
,…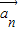 存在n个不全为零的实数k1,k2,…,kn,使得k1
存在n个不全为零的实数k1,k2,…,kn,使得k1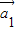 +k2
+k2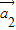 +…,kn
+…,kn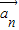 =成立,则称向量
=成立,则称向量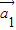 、
、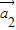 ,…
,…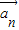 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明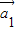 =(1,2),
=(1,2),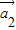 =(1,-1),
=(1,-1),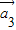 =(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).
=(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).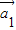 •
•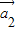 ,…
,…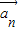 存在n个不全为零的实数k1,k2,…,kn,使得k1
存在n个不全为零的实数k1,k2,…,kn,使得k1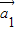 +k2
+k2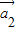 +…,kn
+…,kn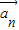 =成立,则称向量
=成立,则称向量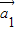 、
、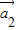 ,…
,…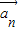 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明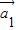 =(1,2),
=(1,2),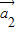 =(1,-1),
=(1,-1),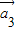 =(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).
=(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况). ,存在n个不全为零的实数k1,k2…,kn,使得
,存在n个不全为零的实数k1,k2…,kn,使得 =
= 成立,则称向量
成立,则称向量 为“线性相关”.依此规定,请你求出一组实数k1,k2,k3的值,它能说明
为“线性相关”.依此规定,请你求出一组实数k1,k2,k3的值,它能说明 =(1,0),
=(1,0), =(1,-1),
=(1,-1), =(2,2)“线性相关”.k1,k2,k3的值分别是 (写出一组即可).
=(2,2)“线性相关”.k1,k2,k3的值分别是 (写出一组即可).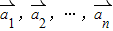 ,存在n个不全为零的实数k1,k2…,kn,使得
,存在n个不全为零的实数k1,k2…,kn,使得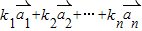 =
=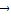 成立,则称向量
成立,则称向量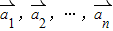 为“线性相关”.依此规定,请你求出一组实数k1,k2,k3的值,它能说明
为“线性相关”.依此规定,请你求出一组实数k1,k2,k3的值,它能说明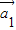 =(1,0),
=(1,0),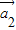 =(1,-1),
=(1,-1),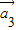 =(2,2)“线性相关”.k1,k2,k3的值分别是 (写出一组即可).
=(2,2)“线性相关”.k1,k2,k3的值分别是 (写出一组即可).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com