
题目列表(包括答案和解析)
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(理)对于数列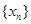 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数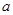 ,公比为正整数
,公比为正整数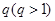 的无穷等比数列
的无穷等比数列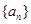 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项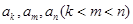 .
.
(1) 若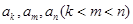 成等比数列,求
成等比数列,求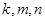 之间满足的等量关系;
之间满足的等量关系;
(2) 他猜想:“在上述数列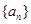 中存在一个子数列
中存在一个子数列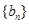 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了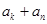 与
与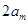 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
(3) 他又想:在首项为正整数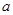 ,公差为正整数
,公差为正整数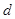 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(理)对于数列 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数 ,公比为正整数
,公比为正整数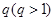 的无穷等比数列
的无穷等比数列 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项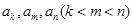 .
.
(1) 若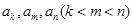 成等比数列,求
成等比数列,求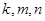 之间满足的等量关系;
之间满足的等量关系;
(2) 他猜想:“在上述数列 中存在一个子数列
中存在一个子数列 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了 与
与 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
(3) 他又想:在首项为正整数 ,公差为正整数
,公差为正整数 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数 ,公比为正整数
,公比为正整数 的无穷等比数列
的无穷等比数列 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项 .
. 成等比数列,求
成等比数列,求 之间满足的等量关系;
之间满足的等量关系; 中存在一个子数列
中存在一个子数列 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了 与
与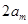 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确; ,公差为正整数
,公差为正整数 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.某高中为调查了解学生体能状况,按年级采用分层抽样的方法从所有学生中抽取360人进行体育达标测试.该校高二年级共有学生1200人,高一、高二、高三三个年级的人数依次成等差数列.
(Ⅰ)若从高一年级中抽取了100人,求从高三年级中抽取了多少人?
(Ⅱ)体育测试共有三个项目:分别是100米跑、立定跳远、掷实心球.已知被抽到的某同学每个项目的测试合格与不合格是等可能的,求该同学三项测试中有且只有两项合格的概率.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
从数列 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 的一个子数列.
的一个子数列.
设数列 是一个首项为
是一个首项为 、公差为
、公差为
 的无穷等差数列.
的无穷等差数列.
(1)若 ,
, ,
, 成等比数列,求其公比
成等比数列,求其公比 .
.
(2)若 ,从数列
,从数列 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若 ,从数列
,从数列 中取出第1项、第
中取出第1项、第
 项(设
项(设 )作为一个等比数列的第1项、第2项,试问当且仅当
)作为一个等比数列的第1项、第2项,试问当且仅当 为何值时,该数列为
为何值时,该数列为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
一. 填空题(每题4分,共48分)
1. {0}; 2. 四; 3. 12; 4. 0; 5. 4; 6. 理 、文7; 7. 理
、文7; 7. 理
 ; 12.
; 12.
 (或
(或 ).
).
二.选择题(每题4分,共16分)
13.D; 14.B; 15.C; 16.理B、文B.
三. 解答题. 17.(本题满分12分)解:由已知得 (3分)
(3分)
∴ , ∴
, ∴ (6分)
(6分)
∴ 又
又 ,即
,即 ,∴
,∴ (9分)
(9分)
∴ 的面积S=
的面积S= .
(12分)
.
(12分)
18.(本题满分12分)解:∵ ,∴
,∴ (5分)
(5分)
∵ ,欲使
,欲使 是纯虚数,
是纯虚数,
而 =
= (7分)
(7分)
∴ , 即
, 即 (11分)
(11分)
∴当 时,
时, 是纯虚数.
(12分)
是纯虚数.
(12分)
19.(本题满分14分,第1小题满分9分,第2小题满分5分)
解:(1)依题意设 ,则
,则 ,
(2分)
,
(2分)
 (4分) 而
(4分) 而 ,
,
∴ ,即
,即 , (6分) ∴
, (6分) ∴ (7分)
(7分)
从而 .
(9分)
.
(9分)
(2) 平面
平面 ,
,
∴直线 到平面
到平面 的距离即点
的距离即点 到平面
到平面 的距离
(2分)
的距离
(2分)
也就是 的斜边
的斜边 上的高,为
上的高,为 .
(5分)
.
(5分)
20.(本题满分14分,第1小题满分8分,第2小题满分6分)
解:(1)不正确.
(2分)
没有考虑到 还可以小于
还可以小于 .
(3分)
.
(3分)
正确解答如下:
令 ,则
,则 ,
,
当 时,
时, ,即
,即 (5分)
(5分)
当 时,
时, ,即
,即 (7分)
(7分)
∴ 或
或 ,即
,即 既无最大值,也无最小值.
(8分)
既无最大值,也无最小值.
(8分)
(2)(理)对于函数 ,令
,令
①当 时,
时, 有最小值,
有最小值, ,
(9分)
,
(9分)
当 时,
时, ,即
,即 ,当
,当 时,即
时,即
∴ 或
或 ,即
,即 既无最大值,也无最小值.
(10分)
既无最大值,也无最小值.
(10分)
②当 时,
时, 有最小值,
有最小值, ,
,
此时, ,∴
,∴ ,即
,即 ,
, 既无最大值,也无最小值 .(11分)
既无最大值,也无最小值 .(11分)
③当 时,
时, 有最小值,
有最小值, ,即
,即 (12分)
(12分)
∴ ,即
,即 ,
,
∴当 时,
时, 有最大值
有最大值 ,没有最小值.
(13分)
,没有最小值.
(13分)
∴当 时,
时, 既无最大值,也无最小值。
既无最大值,也无最小值。
当 时,
时, 有最大值
有最大值 ,此时
,此时 ;没有最小值.
(14分)
;没有最小值.
(14分)
(文)∵ , ∴
, ∴ (12分)
(12分)
∴函数 的最大值为
的最大值为 (当
(当 时)而无最小值. (14分)
时)而无最小值. (14分)
21.(本满分16分,第1、2小题满分各4分,第3小题满分8分)
解:(1) (4分)
(4分)
(2)由 解得
解得 (7分)
(7分)
所以第 个月更换刀具.
(8分)
个月更换刀具.
(8分)
(3)第 个月产生的利润是:
个月产生的利润是: (9分)
(9分)
 个月的总利润:
个月的总利润: (11分)
(11分)
 个月的平均利润:
个月的平均利润: (13分)
(13分)
由  且
且
在第7个月更换刀具,可使这7个月的平均利润 最大(13.21万元) (14分)此时刀具厚度为
最大(13.21万元) (14分)此时刀具厚度为 (mm)
(16分)
(mm)
(16分)
22.(本题满分18分,第1、2小题满分各4分,第3小题满分10分)
解:(1) (4分)
(4分)
(2)各点的横坐标为: (8分)
(8分)
(3)过 作斜率为
作斜率为 的直线
的直线 交抛物线于另一点
交抛物线于另一点 ,
(9分)
,
(9分)
则一般性的结论可以是:
点 的相邻横坐标之和构成以
的相邻横坐标之和构成以 为首项和公比的等比数列(或:点
为首项和公比的等比数列(或:点 无限趋向于某一定点,且其横(纵)坐标之差成等比数列;或:
无限趋向于某一定点,且其横(纵)坐标之差成等比数列;或: 无限趋向于某一定点,且其横(纵)坐标之差成等比数列,等)(12分)
无限趋向于某一定点,且其横(纵)坐标之差成等比数列,等)(12分)
证明:设过点 作斜率为
作斜率为 的直线交抛物线于点
的直线交抛物线于点 由
由
 得
得 或
或 ;
;
 点
点 的横坐标为
的横坐标为 ,则
,则 (14分)
(14分)
于是 两式相减得:
两式相减得: (16分)
(16分)


=

故点 无限逼近于点
无限逼近于点
同理 无限逼近于点
无限逼近于点 (18分)
(18分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com