练习册

  • 练习册
  • 试题
    已知向量..且A为锐角.(1)求角A的大小, 【查看更多】

     

    题目列表(包括答案和解析)

    已知向量a=（sinx，1+cos2x），b=（cosx，），定义函数f（x）=a·b。
    （1）求函数f（x）最小正周期；
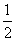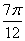    （2）在△ABC中，角A为锐角，且A+B=，f（A）=1，BC=2，求边AC的长。

    查看答案和解析>>

    已知向量a=（x-1，-1），b=（x-m，y），（m∈R），且a·b=0。
    （Ⅰ）将y表示为x的函数y=f（x）；
    （Ⅱ）若tanA、tanB是方程f（x）+4=0的两个实根，A、B是锐角△ABC的两个内角，求证：m≥5；
    （Ⅲ）对任意实数α ，恒有f（2+cosα）≤0，求证：m≥3。

    查看答案和解析>>

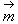    已知向量=（sinA，cosA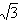），=（，-1），，且A为锐角。
    （1）求角A的大小；
    （2）求函数f（x）=cos2x+4cosAsinx（x∈R）的值域。

    查看答案和解析>>

    已知向量

    设函数

    （I）求函数的最大值及此时x的集合；

    （Ⅱ）在A为锐角的三角形ABC中，角A、B、C的对边分别为a、b、c，且的面积为3，求a的值。

    查看答案和解析>>

    （12分）在锐角三角形ABC中，已知角A、B、C所对的边分别为a、b、c，且，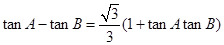

    （1）若c2＝a2＋b2—ab，求角A、B、C的大小；

    （2）已知向量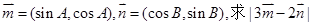的取值范围。

     

     

    查看答案和解析>>

    一、填空题

    1．[]                   2．180                         3．40                   4．5                     5．

    6．15                          7．30                          8．4                     9．                10．

    11．（0 ，）            12．              13．                 14．4

    二、解答题

    15．（1）

                               

                  或

                  或（舍去）……………………………………………………7分

    （2）

                  …………………………………………………………………14分

    16．

              所以OE//平面AA1B1B……………………………………………………………14分

    17．

    18．解：（1）为圆周的点到直线的距离为-------2分

    设的方程为

    的方程为----------------------------------------------------------------5分

    （2）设椭圆方程为，半焦距为c，则

    椭圆与圆O恰有两个不同的公共点，则或 ------------------------------6分

    当时，所求椭圆方程为；-------------8分

    当时，

    所求椭圆方程为-------------------------------------------------------------10分

    （3）设切点为N，则由题意得，在中，，则，

    N点的坐标为，------------------- 11分

    若椭圆为其焦点F1,F2

    分别为点A,B故，-----------------------------------13分

    若椭圆为，其焦点为,

    此时　　　　-------------------------------------------15分

     

     

     

     

     

     

     

     

     

     

    19．

     

    第Ⅱ卷（附加题）参考答案

    21．（1）                                     ………………………………………………4分

       （2） 时对应的向量为 ，时对应的向量为……10分

     

    22．解：（1）由方程的（2）式平方减去（1）式得：　　5分

    （2）曲线的焦点到准线的距离为，离心率为，

    所以曲线的极坐标方程为　　　　　　　　　　　　　　　  　  　10分

    23．解：（1）赋值法：分别令，，得 -----2分

    （2），-------------------------------------------------6分

    （3），的系数为：

    所以，当或时，展开式中的系数最小，为81．----10分

    24．

     


    同步练习册答案