
题目列表(包括答案和解析)
(08年聊城市一模) 给出以下命题:
①合情推理是由特殊到一般的推理,得到的结论不一定正确,演绎推是由一般到特殊的推理,得到的结论一定正确。
②甲、乙两同学各自独立地考察两个变量X、Y的线性相关关系时,发现两人对X的观察数据的平均值相等,都是s,对Y的观察数据的平均值也相等,都是t,各自求出的回归直线分别是l1、l2,则直线l1与l2必定相交于点(s,t)。
③某企业有职工150人,其中高级职称15人,中级职称45人,一般职员90人,若用分层抽样的方法抽出一个容量为30的样本,则一般职员应抽出20人。
④用独立性检验(2×2列联表法)来考察两个分类变量是否有关系时,算出的随机变量K2的值越大,说明“X与Y有关系”成立的可能性越大。
其中真命题的序号是 (写出所有真命题的序号)。
设点 是抛物线
是抛物线

 的焦点,
的焦点, 是抛物线
是抛物线 上的
上的 个不同的点(
个不同的点(
 ).
).
(1) 当 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、 、
、 的坐标,从而使得
的坐标,从而使得
 ;
;
(2)当 时,若
时,若 ,
,
求证: ;
;
(3) 当 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若 ,则
,则 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
【解析】第一问利用抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .
.
由抛物线定义得到
第二问设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


第三问中①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取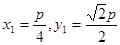 ;
;
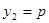 ;
;
 ;
;
解:(1)抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .由抛物线定义得
.由抛物线定义得


因为 ,所以
,所以 ,
,
故可取

 满足条件.
满足条件.
(2)设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


 又因为
又因为



 ;
;
所以

 .
.
(3) ①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取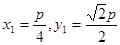 ;
;
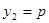 ;
;
 ;
; ,
,
则

 ,
,

 .
.
故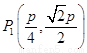 ,
, ,
, ,
, 是一个当
是一个当 时,该逆命题的一个反例.(反例不唯一)
时,该逆命题的一个反例.(反例不唯一)
② 设 ,分别过
,分别过 作
作
抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
,
由 及抛物线的定义得
及抛物线的定义得
 ,即
,即 .
.
因为上述表达式与点 的纵坐标无关,所以只要将这
的纵坐标无关,所以只要将这 点都取在
点都取在 轴的上方,则它们的纵坐标都大于零,则
轴的上方,则它们的纵坐标都大于零,则






 ,
,
而 ,所以
,所以 .
.
(说明:本质上只需构造满足条件且 的一组
的一组 个不同的点,均为反例.)
个不同的点,均为反例.)
③ 补充条件1:“点 的纵坐标
的纵坐标 (
( )满足
)满足  ”,即:
”,即:
“当 时,若
时,若 ,且点
,且点 的纵坐标
的纵坐标 (
( )满足
)满足 ,则
,则 ”.此命题为真.事实上,设
”.此命题为真.事实上,设 ,
,
分别过 作抛物线
作抛物线 准线
准线 的垂线,垂足分别为
的垂线,垂足分别为 ,由
,由 ,
,
及抛物线的定义得 ,即
,即 ,则
,则






 ,
,
又由 ,所以
,所以 ,故命题为真.
,故命题为真.
补充条件2:“点 与点
与点
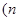 为偶数,
为偶数, 关于
关于 轴对称”,即:
轴对称”,即:
“当 时,若
时,若 ,且点
,且点 与点
与点
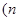 为偶数,
为偶数, 关于
关于 轴对称,则
轴对称,则 ”.此命题为真.(证略)
”.此命题为真.(证略)
已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且抛物线 的焦点为F1.
的焦点为F1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)垂直于OC的直线l与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线l的方程和圆P的方程.
【解析】本试题主要考查了椭圆的方程的求解以及直线与椭圆的位置关系的运用。第一问中,设出椭圆的方程,然后结合抛物线的焦点坐标得到 ,又因为
,又因为 ,这样可知得到
,这样可知得到 。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
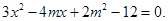 ,再利用
,再利用 可以结合韦达定理求解得到m的值和圆p的方程。
可以结合韦达定理求解得到m的值和圆p的方程。
解:(Ⅰ)设椭圆E的方程为
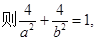 ①………………………………1分
①………………………………1分

 ②………………2分
②………………2分
 ③ 由①、②、③得a2=12,b2=6…………3分
③ 由①、②、③得a2=12,b2=6…………3分
所以椭圆E的方程为 …………………………4分
…………………………4分
(Ⅱ)依题意,直线OC斜率为1,由此设直线l的方程为y=-x+m,……………5分
代入椭圆E方程,得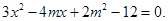 …………………………6分
…………………………6分
 ………………………7分
………………………7分
 、
、 ………………8分
………………8分

 ………………………9分
………………………9分

 ……………………………10分
……………………………10分
当m=3时,直线l方程为y=-x+3,此时,x1 +x2=4,圆心为(2,1),半径为2,
圆P的方程为(x-2)2+(y-1)2=4;………………………………11分
同理,当m=-3时,直线l方程为y=-x-3,
圆P的方程为(x+2)2+(y+1)2=4
已知点 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为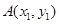 、
、 (其中
(其中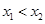 ).
).
(Ⅰ)若 ,求
,求 与
与 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,求圆
相切,求圆 的方程;
的方程;
(Ⅲ)若直线 的方程是
的方程是 ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,
相切,
求圆 面积的最小值.
面积的最小值.
【解析】本试题主要考查了抛物线的的方程以及性质的运用。直线与圆的位置关系的运用。
中∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴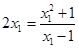 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
(3)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 ,借助于函数的性质圆
,借助于函数的性质圆 面积的最小值
面积的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴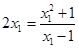 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵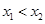 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,则
,则 的斜率
的斜率 ,
,
∴直线 的方程为:
的方程为: ,又
,又 ,
,
∴ ,即
,即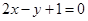 . -----------------7分
. -----------------7分
∵点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即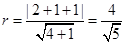 ,--------------8分
,--------------8分
故圆 的面积为
的面积为 . --------------------9分
. --------------------9分
(Ⅲ)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , ………10分
, ………10分
∴
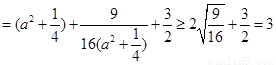 ,
,
当且仅当 ,即
,即 ,
, 时取等号.
时取等号.
故圆 面积的最小值
面积的最小值 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com