
题目列表(包括答案和解析)
(本小题满分12分)
一个袋子内装有若干个黑球,3个白球,2个红球(所有的球除颜色外其它均相同),从中一次性任取2个球,每取得一个黑球得0分,每取一个白球得1分,每取一个红球得2分,用随机变量![]() 表示取2个球的总得分,已知得0分的概率为
表示取2个球的总得分,已知得0分的概率为![]()
(Ⅰ)求袋子内黑球的个数;
(Ⅱ)求![]() 的分布列与期望。
的分布列与期望。
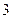 个白球,
个白球, 个红球(所有的球除颜色外其它均相同),从中任取
个红球(所有的球除颜色外其它均相同),从中任取 个球,每取得一个黑球得
个球,每取得一个黑球得 分,每取一个白球得
分,每取一个白球得 分,每取一个红球得
分,每取一个红球得 分,已知得
分,已知得 分的概率为
分的概率为 ,用随机变量X表示取
,用随机变量X表示取 个球的总得分.
个球的总得分.武汉市教育科学研究院命制 2009.4.16
一、选择题
1.B 2.C 3.D 4.A 5.B 6.C 7.A 8.A 9.B 10.D
二、填空题
11.7 12.(2,3) 13. 14. 15.
三、解答题
16.解:(1)由
由知:,于是可知
得.………………………………………………………(6分)
(2)由及
而在上单调递增
可知满足:时单调递增
于是在定义域上的单调递增区间为.………………(12分)
17.解:(1)摸球3次就停止,说明前三次分别都摸到了红球,
则……………………………………………………………(5分)
(2)随机变量的取值为0,1,2,3.
则,
,
.
随机变量的分布列是
0
1
2
3
P
的数学期望为:
.………………………(12分)
18.解:(1)在四棱锥中,底面,则
若,则和面内相交的两直线均垂直
面,故.
在底面的平行四边形中,令
在中,.
于是
在中,由可知:
求得或
依题意,于是有.……………………………………………(6分)
(2)过点作,连结
.
又,面
面
由三垂线定理知:为所求二面角的平面角
过点
易知
又
在中
故所求二面角的大小为45.………………………………………………(12分)
19.解:(1)
故轨迹为以A、B为焦点的双曲线的右支.
设其方程为:
.
故轨迹方程为.…………………………………………(6分)
(2)由
方程有两个正根.
设,由条件知.
而
即
整理得,即
由(1)知,即显然成立.
由(2)、(3)知
而.
.
故的取值范围为……………………(13分)
20.解:(1)由,
求导数得到:
,故在有唯一的极值点
,且知
故上有两个不等实根需满足:
故所求m的取值范围为.………………………………………(6分)
(2)又有两个实根
则
两式相减得到:
于是
,故
要证:,只需证:
只需证:
令,则
只需证明:在上恒成立.
又则
于是由可知.故知
上为增函数,则
从而可知,即(*)式成立,从而原不等式得证.……………
……………………………………………………………(13分)
21.解:(1)经过计算可知:
.
求得.…………………………………………(4分)
(2)由条件可知:.…………①
类似地有:.…………②
①-②有:.
即:.
因此:
即:故
所以:.…………………………………………(8分)
(3)假设存在正数,使得数列的每一项均为整数.
则由(2)可知:…………③
由,及可知.
当时,为整数,利用,结合③式,反复递推,可知,,,,…均为整数.
当时,③变为………④
我们用数学归纳法证明为偶数,为整数
时,结论显然成立,假设时结论成立,这时为偶数,为整数,故为偶数,为整数,所以时,命题成立.
故数列是整数列.
综上所述,的取值集合是.………………………………………(13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com