
题目列表(包括答案和解析)
(本小题12分)设有数列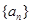 ,
,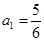 ,若以
,若以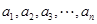 为系数的二次方程
为系数的二次方程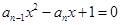 都有根
都有根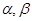 ,且满足
,且满足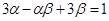 。
。
(1)求证:数列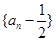 是等比数列。
是等比数列。
(2)求数列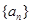 的通项
的通项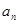 以及前n项和
以及前n项和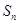 。
。
(本大题14分)
已知![]()
![]()
![]()
![]() ,且
,且![]()
![]() ·
·![]() +
+![]() ,
,
(1)将函数![]() 的表达式化为
的表达式化为![]() 的形式;
的形式;
(2)求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(3)当![]()
![]() 的最小值为0,求此时函数
的最小值为0,求此时函数![]() 的最大值, 并求出相应的
的最大值, 并求出相应的![]() 的值。
的值。
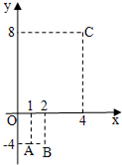 已知数列{an}的前n 项和Sn是关于n(n∈N*)的二次函数,其图象经过三点A,B,C(如图所示).
已知数列{an}的前n 项和Sn是关于n(n∈N*)的二次函数,其图象经过三点A,B,C(如图所示).| 3 |
(本小题10分)已知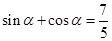 ,且
,且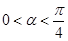 .
.
(Ⅰ)求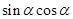 、
、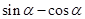 的值;
的值;
(Ⅱ)求 的值.
的值.
一、填空题
1. ;2. 110;3. ;4. ①③;5. ③;6. 10.5亿元;
7. 81; 8. ;
9. 一条边的平方等于其它两条边平方和的三角形是直角三角形;
10. ;
11. ;12. ;13. ;14. 60
二、解答题
15. 解:(1)由可得m=1; …………4分
(2)由可得m=0; …………8分
(3)由可得m=2; …………12分
综上:当m=1时,复数是0;当m=1时,复数是纯虚数;当m=2,复数是.
…………14分
16. 解:(Ⅰ); …………4分
(Ⅱ)是以4为其一个周期的周期函数. …………6分
∵, …………10分
∴, …………12分
所以是周期函数,其中一个周期为4. …………14分
17. 解:(1)只有一个盒子空着,则有且只有一个盒子中投放两个球,另外3只盒子中各投放一个球,先将球分成2,1,1,1的四组,共有种分法, …………4分
再投放到五个盒子的其中四个盒子中,共有种放法,所以满足条件的投放方法共有=1200(种); …………8分
(2)五个球投放到五个盒子中,每个盒子中只有一个球,共有种投放方法,
而球的编号与盒子编号全相同的情况只有一种,所以球的编号与盒子编号不全相同的投放方法共有=119(种). …………14分
18. 证明:记=…(,>1), …………2分
(1)当=2时,>,不等式成立; …………6分
(2)假设=(,≥2)时,不等式成立, …………8分
即=…>,
则当=+1时,有=+>+=
>= …………12分
∴当=+1时,不等式也成立. …………14分
综合(1),(2)知,原不等式对任意的(>1)都成立. …………16分
19. 解:(Ⅰ)由=10,=20,=5.2,
可得, …………4分
∴年推销金额与工作年限之间的相关系数约为0.98. …………6分
(Ⅱ) 由(Ⅰ)知,>,
∴可以认为年推销金额与工作年限之间具有较强的线性相关关系. …………8分
设所求的线性回归方程为,则. …………10分
∴年推销金额关于工作年限的线性回归方程为. …………12分
(Ⅲ) 由(Ⅱ) 可知,当时, = 0.5×11+ 0.4 = 5.9万元,
∴可以估计第6名推销员的年推销金额为5.9万元. …………16分
20. 解:(1)设(), …………2分
则集合{?}={?},
故表示以(0,3)为圆心,2为半径的圆; …………6分
设(),()且,…………8分
则 …………10分
将代入得,
故表示以(-6,0)为圆心,4为半径的圆; …………12分
(2)表示分别在圆上的两个动点间的距离,又圆心距>2+4,
故最大值为6+3,最小值为3-6. …………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com