设△ABC的内角A、B、C所对的边分别为a、b、c，已知a＝1，b＝2，cosC＝. (1)求△ABC的周长；       (2)求cos(A－C)的值．

【解析】（1）借助余弦定理求出边c，直接求周长即可.（2）根据两角差的余弦公式需要求sinC,sinA,cosA,由正弦定理即可求出sinA,进而可求出cosA.sinC可由cosA求出，问题得解.

在△ABC中，a、b、c分别是角A、B、C的对边,cosB＝.

⑴ 若cosA＝－,求cosC的值；  ⑵ 若AC＝,BC＝5，求△ABC的面积.

【解析】第一问中sinB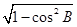＝＝, sinA＝＝

cosC＝cos(180°－A－B)＝－cos(A＋B)                ＝sinA.sinB－cosA·cosB

＝×－(－)×＝

第二问中，由＝＋－2AB×BC×cosB得 10＝＋25－8AB

解得AB＝5或AB＝3综合得△ABC的面积为或

解：⑴ sinB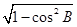＝＝, sinA＝＝,………………2分

∴cosC＝cos(180°－A－B)＝－cos(A＋B)                  ……………………3分

＝sinA.sinB－cosA·cosB                            ……………………4分

＝×－(－)×＝                   ……………………6分

⑵ 由＝＋－2AB×BC×cosB得 10＝＋25－8AB   ………………7分

解得AB＝5或AB＝3，                               ……………………9分

若AB＝5，则S_△ABC＝AB×BC×sinB＝×5×5×＝    ………………10分

若AB＝3，则S_△ABC＝AB×BC×sinB＝×5×3×＝……………………11分

综合得△ABC的面积为或

在△ABC中，若sinA＝，cosB＝，求cosC.

（本小题满分14分）已知锐角中的三个内角分别为．

（1）设·＝·，求证：是等腰三角形；

（2）设向量＝(2sinC, －), ＝(cos2C, 2cos2 －1), 且∥, 若sinA＝，求sin(－B)的值．

在三角形ＡＢＣ中，若sinA.＝，，则的值是（    ）

A.           B.          Ｃ.或　     Ｄ.