题目列表(包括答案和解析)
（本小题满分12分）椭圆
的中心为坐标原点
，焦点在
轴上，焦点到相应准线的距离以及离心率均为
，直线
与轴交于点
，与椭圆交于相异两点
、
，且
．（1）求椭圆方程；（2）若
，求
的取值范围．
（本小题满分12分）椭圆C的中心在坐标原点，焦点在x轴上，右焦点F的坐标为（2，0），右准线方程为
（I）求椭圆C的方程； （II）过点F作斜率为k的直线l，与椭圆C交于A、B两点，若
，求k的取值范围。
（本小题满分12分）
椭圆C的中心在坐标原点，焦点在x轴上，右焦点F的坐标为（2，0），且点F到短轴的一个端点的距离是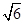
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F作斜率为k的直线l，与椭圆C交于A、B两点，若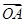
·
＞－
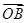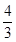，求k的取值范围．
（本小题满分12分）椭圆E的中心在坐标原点O，焦点在x轴上，离心率为
．点P（1，
）、A、B在椭圆E上，且
（m∈R）；
（Ⅰ）求椭圆E的方程及直线AB的斜率；
（Ⅱ）求证：当△PAB的面积取得最大值时，原点O是△PAB的重心。
（本小题满分12分）椭圆E的中心在坐标原点O，焦点在x轴上，离心率为
．点P（1，
）、A、B在椭圆E上，且
（m∈R）；
（Ⅰ）求椭圆E的方程及直线AB的斜率；
（Ⅱ）求证：当△PAB的面积取得最大值时，原点O是△PAB的重心。
1．B 2．B 3．A 4．C 5．C 6．B 7．D 8．B 9．C 10．B
11．A 12．D
【解析】
1．，所以选B．
2．的系数是，所以选B．
3．，所以选．
4．为钝角或，所以选C
5．，所以选C．
6．，所以选B．
7．，所以选D．
8．化为或，所以选B．
9．将左移个单位得，所以选A．
10．直线与椭圆有公共点，所以选B．
11．如图，设，则，
,
,从而，因此与底面所成角的正弦值等于．所以选A．
12．画可行域 可知符合条件的点是：共6个点，故，所以选D．
二、
13．185．．
14．60．．
15．，由，得
．
16．．如图：
如图，可设，又，
．
当面积最大时，．点到直线的距离为．
三、
17．（1）由三角函数的定义知：．
（2）
．
18．（1）设两年后出口额恰好达到危机前出口额的事件为，则．
（2）设两年后出口额超过危机前出口额的事件为，则．
19．（1）设与交于点．
从而，即，又，且
平面为正三角形，为的中点，
，且，因此，平面．
（2）平面，∴平面平面又，∴平面平面
设为的中点，连接，则，
平面，过点作，连接，则．
为二面角的平面角．
在中，．
又．
20．（1）
（2）
又
综上：．
21．（1）的解集为（1，3）
∴1和3是的两根且
由此得
时，时，
在处取得极小值
③
由式①、②、③联立得：
．
（2）
∴当时，在上单调递减，
当时，
当时，在[2，3]上单调递增，
22．（1）由得
∴椭圆的方程为：．
（2）由得，
又
设直线的方程为：
由得
由此得． ①
设与椭圆的交点为，则
由得
，整理得
，整理得
时，上式不成立， ②
由式①、②得
或
∴取值范围是．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com