练习册

  • 练习册
  • 试题
    C． D．不确定 【查看更多】

     

    题目列表(包括答案和解析)

    确定一个平面的条件是

    [　　]

    A．空间三点

    B．空间两条件直线

    C．一条直线和一点

    D．不过同一点且两两相交的三条直线

    查看答案和解析>>

    定义在R上的奇函数f(x)为增函数，偶函数g(x)在区间［0，+∞)的图像与f(x)的图像重合，设a＞b＞0，给出下列不等式，其中正确不等式的序号是(    )

    ①f(b)－f(－a)＞g(a)－g(－b)  ②f(b)－f(－a)＜g(a)－g(－b) 

    ③f(a)－f(－b)＞g(b)－g(－a)  ④f(a)－f(－b)＜g(b)－g(－a)

    A．①③               B.②④          C.①④                 D.②③

    查看答案和解析>>

    定义在R上的函数f（x），如果存在函数g（x）=kx+b（k，b为常数），使得f（x）≥g（x）对一切实数x都成立，则称g（x）为函数f（x）的一个承托函数、现有如下命题：
    ①对给定的函数f（x），其承托函数可能不存在，也可能有无数个；②g（x）=2x为函数f（x）=2x的一个承托函数；③定义域和值域都是R的函数f（x）不存在承托函数．
    下列选项正确的是


    1. A.
      ①
    2. B.
      ②
    3. C.
      ①③
    4. D.
      ②③

    查看答案和解析>>




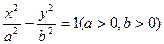
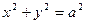
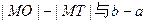
    A．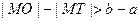
    B．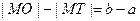
    C．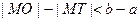
    D．大小关系不确定

    查看答案和解析>>

    给定下列两个关于异面直线的命题：
    命题Ⅰ：若平面 α 上的直线 a 与平面 β 上的直线 b 为异面直线，直线 c 是 α 与β　的交线，那么，c 至多与 a，b 中的一条相交；
    命题Ⅱ：不存在这样的无穷多条直线，它们中的任意两条都是异面直线．
    那么，


    1. A.
      命题Ⅰ正确，命题Ⅱ不正确
    2. B.
      命题Ⅱ正确，命题Ⅰ不正确
    3. C.
      两个命题都正确
    4. D.
      两个命题都不正确

    查看答案和解析>>

    一、填空题：中国数学论坛网 http://www.mathbbs.cn 2008年03月18日正在开通

    1．2   2．11   3．3   4．   5．5   6．―2   7．   8．   9．18

    2,4,6

    二、选择题：

    13．C   14．D   15．D   16．B

    三、解答题：

    17．解：设的定义域为D，值域为A

        由                                                         …………2分

                            …………4分

        又                                                    …………6分

                                                              …………8分

        的定义域D不是值域A的子集

        不属于集合M                                                             …………12分

    18．解：如图建立空间直角坐标系

    ∵由题意可知∠C1AC=60°，C1C=  …………2分

    、、、               …………4分

    即                                …………6分

    设

    则                                           …………8分

                         …………10分

                …………12分

    19．解：（1）                                             …………2分

                                 …………4分

                   …………6分

       （2）设                                        …………8分

    则  …………10分

    （m2）      …………12分

    答：当（m2）   …………14分

    20．解：（1）=3

                                                                    …………2分

    设圆心到直线l的距离为d，则

    即直线l与圆C相离                                                   …………6分

       （2）由  …………8分

    由条件可知，                                        …………10分

    又∵向量的夹角的取值范围是[0，π]

                                                               …………12分

                                                           …………14分

    21．解：（1）

       

                                    …………4分

       （2）                                   …………5分

       

                                                               …………8分

                                          …………10分

       （3）

                                                           …………12分

       

        故103不是数列中的项                                                 …………16分

    22．解：（1）易知                             …………2分

       

                                                    …………4分

       （2）

       

         （*）                                                         …………6分

       

        同理                                                                                        …………8分

       

                                                                             …………10分

       （3）

        先探索，当m=0时，直线L⊥ox轴，则ABED为矩形，由对称性知，AE与BD相交于FK中点N

        且                                                                      …………11分

        猜想：当m变化时，AE与BD相交于定点         …………12分

        证明：设

        当m变化时首先AE过定点N

     

       

        ∴KAN=KEN   ∴A、N、E三点共线

        同理可得B、N、D三点共线

        ∴AE与BD相交于定点                                      …………18分

     


    同步练习册答案