
题目列表(包括答案和解析)
 函数y1=-
函数y1=-
| ||
| x |
2
| ||
| x |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
把函数图象先往左侧平移2个单位,再往上平移1各单位,则不同类型函数解析式的变化可举例如下:
y=3x2→y=3(x+2)2+1;y=3x3→y=3(x+2)3+1;y=3 →y=3
→y=3 +1;y=3
+1;y=3 →y=3
→y=3 +1;
+1;
y= →y=
→y= +1;…
+1;…
(1)若把函数y= +1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y=
+1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y= +1;
+1;
(2)分析下列关于函数y= +1图象性质的描述:
+1图象性质的描述:
①图象关于(1,1)点中心对称;②图象必不经过第二象限;③图象与坐标轴共有2个交点;④当x>0时,y随着x取值的变大而减小.其中正确的是: ___ .(填序号)
把函数图象先往左侧平移2个单位,再往上平移1各单位,则不同类型函数解析式的变化可举例如下:
y=3x2→y=3(x+2)2+1;y=3x3→y=3(x+2)3+1;y=3 →y=3
→y=3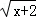 +1;y=3
+1;y=3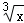 →y=3
→y=3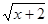 +1;
+1;
y=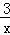 →y=
→y=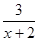 +1;…
+1;…
(1)若把函数y=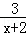 +1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y=
+1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y=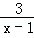 +1;
+1;
(2)分析下列关于函数y=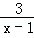 +1图象性质的描述:
+1图象性质的描述:
①图象关于(1,1)点中心对称;②图象必不经过第二象限;③图象与坐标轴共有2个交点;④当x>0时,y随着x取值的变大而减小.其中正确的是: ___ .(填序号)
 →y=3
→y=3 +1;y=3
+1;y=3 →y=3
→y=3 +1;
+1; →y=
→y= +1;…
+1;… +1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y=
+1图象再往 _________ 平移 _______ 个单位,所得函数图象的解析式为y= +1;
+1; +1图象性质的描述:
+1图象性质的描述:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com