
题目列表(包括答案和解析)
(本小题满分16分)已知数列![]() 的各项均为正数,
的各项均为正数,![]() 表示该数列前
表示该数列前![]() 项的和,且对任意正整数
项的和,且对任意正整数![]() ,恒有
,恒有![]() ,设
,设![]() .
.
(1)求![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)求数列![]() 的最小项.
的最小项.
(本小题满分16分)已知数列![]() 是以
是以![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为公比的等比数列.
为公比的等比数列.
(Ⅰ)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,求整数
,求整数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列![]() 中是否存在一项
中是否存在一项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续![]() 项的和?请说明理由;
项的和?请说明理由;
(Ⅲ)若![]() (其中
(其中![]() ,且(
,且(![]() )是(
)是(![]() )的约数),
)的约数),
求证:数列![]() 中每一项都是数列
中每一项都是数列![]() 中的项.
中的项.
(本小题满分16分)已知数列![]() 是以
是以![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,求整数
,求整数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列![]() 中是否存在一项
中是否存在一项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续![]() 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若![]() (其中
(其中![]() ,且(
,且(![]() )是(
)是(![]() )的约数),求证:数列
)的约数),求证:数列![]() 中每一项都是数列
中每一项都是数列![]() 中的项.
中的项.
(本小题满分16分)
已知数列 是等差数列,数列
是等差数列,数列 是等比数列,且对任意的
是等比数列,且对任意的 ,都有
,都有 .
.
(1)若 的首项为4,公比为2,求数列
的首项为4,公比为2,求数列 的前
的前 项和
项和 ;
;
(2)若 .
.
①求数列 与
与 的通项公式;
的通项公式;
②试探究:数列 中是否存在某一项,它可以表示为该数列中其它
中是否存在某一项,它可以表示为该数列中其它 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由.
(本小题满分16分)
已知数列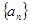 中,
中,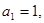 且点
且点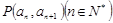 在直线
在直线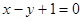 上.
上.
(1)求数列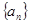 的通项公式;
的通项公式;
 (2)若函数
(2)若函数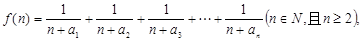 求函数
求函数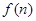 的最小值;
的最小值;
(3)设 表示数列
表示数列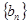 的前
的前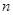 项和.试问:是否存在关于
项和.试问:是否存在关于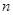 的整式
的整式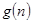 ,使得
,使得
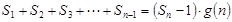 对于一切不小于2的自然数
对于一切不小于2的自然数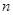 恒成立? 若存在,写出
恒成立? 若存在,写出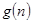 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
数 学
1.24 2.64 3. 4. -1 5. 6. 7. (-∞,-1][3,+∞)
8. 4x+y-6=0或3x+2y-7=0 9. 九或十六 10. 2 11. 2n-1 12.
13. { |-<<-}
14. >
15. 解:(1)当截距不为零时,设所求直线方程为,即x+y-a=0,??????(1分)
因为点M(4,3)与所求直线的距离为5,所以,解得a=7±5,??????(5分)
此时所求直线方程为x+y-7-5=0,或x+y-7+5=0??????(6分)
(2)当截距为零时,设所求直线为y=kx,??????(7分)
因为,即(4k-3)2=25(k2+1),解得k=-,??????(11分)
此时所求直线方程为y=-x . ??????(12分)
综上所述,所求直线方程为x+y-7-5=0,或x+y-7+5=0,或y=-x ??????(14分).
16.解:(1)∵ s10=a1+a2+????+a10
S22= a1+a2+????+a22, 又s10= S22
∴a11+a2+????+a22 =0 ?????? (3分)
,即a11+a22=2a1+31d=0, 又a1=31,
∴ d=-2 ?????? (6分)
∴ ??????(9分)
(2)解法一:由(1)∵sn=32n-n2
∴当n=16时,sn有最大值,sn的最大值是256。 ???????????? (14分)
解法二:由sn=32n-n2=n(32-n),欲使sn有最大值,应有1<n<32,
从而, ??????(13分)
当且仅当n=32-n,即n=16时,sn有最大值256 ??????(14分)
17. 解:(1)f(1)=-3+a(6-a)+b=-a2+6a+b-3, ??????(1分)
∵f(1)>0,∴a2-6a+3-b<0, ??????(2分)
△=24+4b,当b≤-6,即△≤0时,f(1)>0的解集为;??????(5分)
当b<-6,即△>0时,由2-6a+3-b<0,解得,3-<a<3+??????(8分)
综上所述:当b≤-6时,f(1)>0的解集为;当b>-6时,不等式的解集为(3-,3+). ??????(9分)
(2)∵不等式-3x2+a(6-a)x+b>0的解集为(-1,3),
∴, ??????(11分)
解得 ??????(14分)
18.解:由题意,对于甲车,有0.1x+0.001x2>12, ??????(2分)
即 x2+10x-1200>0,
解得x>30或x<-40(不合实际意义,舍去) ??????(6分)
这表明甲车的车速超过30km/h.但根据题意刹车距离略超过12m,由此估计甲车不会超过限速40km/h ??????(8分)
对于乙车,有
0.05x+0.005x2>10, ??????(10分)
即x2+10x-2000>0,
解得x>40,或x<-50(不合实际意义,舍去) ??????(14分)
这表明乙车的车速超过40km/h,超过规定限速。 ??????(16 分)
19.解:(1)由2sin2A-cos2A-2=0,得cos2A=-,??????(3分)
又0<A<,则2A=,故A= ??????(5分)
(2)由(1)及已知得B+C=,又C(,),可得0<B<??????(8分)
设△ABC的外接圆半径为R,则b+c-=2R(sinB+sinC-)
=2R[sinB+sin(-B)-]
=2R(sinB+sincosB-cossinB-)
=2R(sinB+cosB-)=2R[sin(B+)-], ??????(13分)
∵0<B<,∴,∴<sin(B+)<,∴b+c<a. ??????(16分)
20.解:(1)∵a1=1,
∴b1=5-2=3, ??????(2分)
由,得,
两式相减得, ??????(4分)
即,亦即 ??????(6分)
??????(8分)
∴对nN恒成立,∴{bn}为首项为3,公比为2的等比数列?????(10分)
(2)由(1)得bn=3?2n-1,∵bn=an+1-2an
∴ ??????(12分)
∴,即,又 c1= ??????(15分)
∴{}为首项为,公差为的等差数列. ??????(16分)
 17.
17.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com