
题目列表(包括答案和解析)

24图所示为某种电子秤的原理示意图,AB为一均匀的
滑线变阻器,阻值为R,长度为L,两边分别有P1、P2两个
滑动头,与P1相连的金属细杆可在被固定的竖直光滑绝缘
杆MN上保持水平状态,金属细杆与托盘相连,金属细杆
|
P1、P2间出现电压时,该电压经过放大,通过信号转换后
在显示屏上显示出质量的大小.已知弹簧的劲度系数为k,托盘自身质量为m0,电源的电动势为E,电源的内阻忽略不计,信号放大器、信号转换器和显示器的分流作用忽略不计.求:
(1)托盘上未放物体时,在托盘的自身重力作用下,P1距A端的距离x1;
(2)在托盘上放有质量为m的物体时,P1距A端的距离x2;
(3)在托盘上未放物体时通常先校准零点,其方法是:调节P2,从而使P1、P2间的电压为零.校准零点后,将被称物体放在托盘上,试推导出被称物体的质量m与P1、P2间电压U的函数关系式.
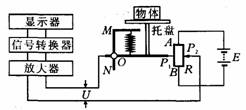
24图所示为某种电子秤的原理示意图,AB为一均匀的
滑线变阻器,阻值为R,长度为L,两边分别有P1、P2两个
滑动头,与P1相连的金属细杆可在被固定的竖直光滑绝缘
杆MN上保持水平状态,金属细杆与托盘相连,金属细杆
|
P1、P2间出现电压时,该电压经过放大,通过信号转换后
在显示屏上显示出质量的大小.已知弹簧的劲度系数为k,托盘自身质量为m0,电源的电动势为E,电源的内阻忽略不计,信号放大器、信号转换器和显示器的分流作用忽略不计.求:
(1)托盘上未放物体时,在托盘的自身重力作用下,P1距A端的距离x1;
(2)在托盘上放有质量为m的物体时,P1距A端的距离x2;
(3)在托盘上未放物体时通常先校准零点,其方法是:调节P2,从而使P1、P2间的电压为零.校准零点后,将被称物体放在托盘上,试推导出被称物体的质量m与P1、P2间电压U的函数关系式.
题24图中A、B之间为一峡谷,相距2d,C为固定在悬崖上的一根横梁,一箩筐D通过两根轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷AB的正中央,且和峡谷两边的平地差不多在同一水平面上.已知筐的质量为M,每根绳的长度都是l,筐的大小和d相比可忽略不计.现有一人位于峡谷的一边A处,他想到达峡谷的对岸B处,在他身边有很多质量差不多都是m的石块,于是他便不断把石块抛入箩筐,使箩筐动起来,当筐摆恰好到A处时(轻绳与竖直方向夹角未超过10??),他就跨入筐中,当筐摆到B处时,再跨出筐到达B处.如果此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央,石块击中筐后随即落在筐内并和筐一起运动,石块击筐的时刻,其速度的大小为v0,方向都是水平的,不计空气阻力,重力加速度为g,试求:
(1)此人从A处进入箩筐到摆动至B处经过的时间.
(2)要使筐摆到A处,此人至少需向箩筐中扔的石块数.
(18分)
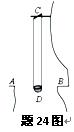
题24图中A、B之间为一峡谷,相距2d,C为固定在悬崖上的一根横梁,一箩筐D通过两根轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷AB的正中央,且和峡谷两边的平地差不多在同一水平面上.已知筐的质量为M,每根绳的长度都是l,筐的大小和d相比可忽略不计.现有一人位于峡谷的一边A处,他想到达峡谷的对岸B处,在他身边有很多质量差不多都是m的石块,于是他便不断把石块抛入箩筐,使箩筐动起来,当筐摆恰好到A处时(轻绳与竖直方向夹角未超过10º),他就跨入筐中,当筐摆到B处时,再跨出筐到达B处.如果此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央,石块击中筐后随即落在筐内并和筐一起运动,石块击筐的时刻,其速度的大小为v0,方向都是水平的,不计空气阻力,重力加速度为g,试求:
(1)此人从A处进入箩筐到摆动至B处经过的时间.
(2)要使筐摆到A处,此人至少需向箩筐中扔的石块数.
(18分)
题24图中A、B之间为一峡谷,相距2d,C为固定在悬崖上的一根横梁,一箩筐D通过两根轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷AB的正中央,且和峡谷两边的平地差不多在同一水平面上.已知筐的质量为M,每根绳的长度都是l,筐的大小和d相比可忽略不计.现有一人位于峡谷的一边A处,他想到达峡谷的对岸B处,在他身边有很多质量差不多都是m的石块,于是他便不断把石块抛入箩筐,使箩筐动起来,当筐摆恰好到A处时(轻绳与竖直方向夹角未超过10º),他就跨入筐中,当筐摆到B处时,再跨出筐到达B处.如果此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央,石块击中筐后随即落在筐内并和筐一起运动,石块击筐的时刻,其速度的大小为v0,方向都是水平的,不计空气阻力,重力加速度为g,试求:
(1)此人从A处进入箩筐到摆动至B处经过的时间.
(2)要使筐摆到A处,此人至少需向箩筐中扔的石块数.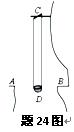
一.1、10,8, 2、5,2.8, 3、mgtanq/2NLI,mgsinq/2NLI, 4、800,与x、y轴负向都夹45°角, 5、(2n+1/3)pN rad/s(n∈N),(2n+5/3)pN rad/s(n∈N),
二.6、C, 7、C, 8、A, 9、A, 10、B,
三.11、C、D, 12、A、D, 13、B、C、D, 14、B、C,
四.15、(BC),磁场总是要阻碍 16、l+d/2,2t/(n-1),p2(n-1)2(
五.20、(1)1.5V,b点高,(2)
21.(1)1.1´105Pa,(2)1.2´105Pa,(3)20J,
22.(1)v0=,(2)乙正确,设小球垂直击中环,则其速度方向必过圆心,设其与水平方向的夹角为q,Rsinq=gt2/2,R(1+cosq)=v0t,且tanq=gt/v0可解得q=0,但这是不可能的,
23.(1)此时vB=vC,由机械能守恒得:mgR=´3mvB2,即vB=vC=,(2)此时直杆竖直方向速度为零,由机械能守恒得:mgh=´2mvB2,h=R,(3)W=-mvC2=-mgR,
24.(1)A释放后有qE+f=ma,得f=0.2N,A速度减到零,t=vA0/a=2s,经过的位移为s=vA02/
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com