
题目列表(包括答案和解析)
已知方程y=bx+a是两个具有线性相关关系的变量的一组数据(x1,y1),(x2,y2),…,(x10,y10)的回归方程,则“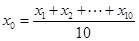 ,
, ”是“(x0,y0)满足线性回归方程y=bx+a”的( )
”是“(x0,y0)满足线性回归方程y=bx+a”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 ,
, ”是“(x0,y0)满足线性回归方程y=bx+a”的( )
”是“(x0,y0)满足线性回归方程y=bx+a”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 |
| y |
 |
| y |
| x1+x2+…+x10 |
| 10 |
| y1+y2+…+y10 |
| 10 |
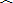 |
| y |
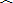 |
| y |
| x1+x2+…+x10 |
| 10 |
| y1+y2+…+y10 |
| 10 |
 ,则“(x,y)满足线性回归方程
,则“(x,y)满足线性回归方程 ”是“
”是“ ,
, ”的 .条件.(填充分不必要、必要不充分、充要)
”的 .条件.(填充分不必要、必要不充分、充要)一、ABCBD BCABD
二、11.2 12.  13.4 14.10 15. ①②③
13.4 14.10 15. ①②③
三、16. 解:(1) ,
3分
,
3分
由已知 ,得
,得 .
6分
.
6分
(2)由(1)得 ,
8分
,
8分
 当
当 时,
时, 的最小值为
的最小值为 ,
10分
,
10分
由 ,得
,得 值的集合为
值的集合为 . 13分
. 13分
17. 解:(I)取AB的中点O,连接OP,OC  PA=PB
PA=PB  PO
PO AB
AB
又在 中,
中, ,
,
在 中,
中, ,又
,又 ,故有
,故有
 又
又 ,
,
 面ABC 4分
面ABC 4分
又 PO 面PAB,
面PAB, 面PAB
面PAB 面ABC
6分
面ABC
6分
(Ⅱ)以O为坐标原点,
分别以OB,OC,OP为 轴,
轴, 轴,
轴, 轴建立坐标系,
轴建立坐标系,
 如图,则A
如图,则A 8分
8分


设平面PAC的一个法向量为 。
。
 得
得
令 ,则
,则
 11分
11分
设直线PB与平面PAC所成角为 ,
,
于是 13分
13分
18. 解:(1) ;
4分
;
4分
(2)消费总额为1500元的概率是: 5分
5分
消费总额为1400元的概率是: 6分
6分
消费总额为1300元的概率是:
 =
= ,
,
所以消费总额大于或等于1300元的概率是 ;
8分
;
8分
(3) ,
,
 ,
,
 =
=
 。所以
。所以 的分布列为:
的分布列为:

0
1
2
3

0.294
0.448
0.222
0.036
数学期望是: 。 13分
。 13分
19. 解:∵ 的右焦点
的右焦点
∴椭圆的 ,
,  .椭圆方程为
.椭圆方程为 .
.
(Ⅰ)当 时,故椭圆方程为
时,故椭圆方程为 , 3分
, 3分
(Ⅱ)依题意设直线 的方程为:
的方程为: ,
,
联立 得点
得点 的坐标为
的坐标为 . 4分
. 4分
将 代入
代入 得
得 .
.
设 、
、 ,由韦达定理得
,由韦达定理得 ,
, . 5分
. 5分
又 ,
, .
.

 7分
7分
 有实根, ∴点
有实根, ∴点 可以在圆上. 8分
可以在圆上. 8分
(Ⅲ)假设存在满足条件的实数 ,
,
由 解得:
解得: . 10分
. 10分
∴ ,
, ,又
,又 .即
.即 的边长分别是
的边长分别是 、
、 、
、 .
.
 时,能使
时,能使 的边长是连续的自然数。 1
的边长是连续的自然数。 1 3分
3分
20. 解:(1) .
1分
.
1分
当 时,
时, ,
, 在
在 上单调递增;
2分
上单调递增;
2分
当 ,
, 时,
时, ,
, 在
在 上单调递减;
上单调递减;
 时,
时, ,
, 在
在 上单调递增.
3分
上单调递增.
3分
综上所述,当 时,
时, 的单调递增区间为
的单调递增区间为 ;当
;当 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .
4分
.
4分
(2)充分性: 时,由(1)知,
时,由(1)知, 在x=1处有极小值也是最小值,
在x=1处有极小值也是最小值,
即 。而
。而 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以 在
在 上有唯一的一个零点x=1. 6分
上有唯一的一个零点x=1. 6分
必要性:若函数f(x)存在唯一零点,即方程 =0在
=0在 上有唯一解,
上有唯一解,
因 , 由(1)知,
, 由(1)知, 在
在 处有极小值也是最小值f(a),
处有极小值也是最小值f(a),
 f(a)=0,即
f(a)=0,即 .
7分
.
7分
令 ,
,  .
.
当 时,
时, ,
, 在上单调递增;当
在上单调递增;当 时,
时, ,
,
 在
在 上单调递减。
上单调递减。
 ,
, =0只有唯一解
=0只有唯一解 .
.
因此 =0在
=0在 上有唯一解时必有
上有唯一解时必有 .
.
综上:在 时,
时,  =0在
=0在 上有唯一解的充要条件是
上有唯一解的充要条件是 . 9分
. 9分
(3)证明:∵1<x<2, ∴ .
.
令 ,∴
,∴
 ,11分
,11分
由(1)知,当 时,
时, ,∴
,∴ ,
,
∴ .∴
.∴ ,
12分
,
12分
∴F(x)在(1,2)上单调递增,∴ ,
,
∴ 。∴
。∴ .
14分
.
14分
21. (Ⅰ)解:考虑在矩阵 作用下,求出变换后的三角形的顶点坐标,从而求得三角形的面积,可先求得
作用下,求出变换后的三角形的顶点坐标,从而求得三角形的面积,可先求得 ,由
,由
 =
= ,得点
,得点 在矩阵
在矩阵 作用下变换所得到的点
作用下变换所得到的点 ,同理求得
,同理求得 在矩阵
在矩阵 作用下变换所得到的点分别是
作用下变换所得到的点分别是 ,
, ,计算得△
,计算得△ 的面积为3.
7分
的面积为3.
7分
(Ⅱ)解:直线 的极坐标方程
的极坐标方程 ,则
,则 ,
,
即 ,所以直线
,所以直线 的直角坐标方程为
的直角坐标方程为 ; 2分
; 2分
设 ,其中
,其中 ,则P到直线
,则P到直线 的距离
的距离
 ,其中
,其中 ,∴ 当
,∴ 当 时,
时, 的最大值为
的最大值为 ;当
;当 时,
时, 的最小值为
的最小值为 。
7分
。
7分
(Ⅲ)解:由柯西不等式,得 , 2分
, 2分
即 .由条件,得
.由条件,得 .解得
.解得 , 2分
, 2分
当且仅当 时等号成立.代入
时等号成立.代入 时,
时, ;
; 时,
时, .所以,
.所以, 的取值范围是
的取值范围是 .
7分
.
7分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com