
题目列表(包括答案和解析)
考点:作图-轴对称变换。
专题:作图题。
分析:分别找出三角形关于直线l的对称点,然后顺次连接即可.
解答:解:如图所示,红色三角形即为要求作的关于直线l的对称三角形.
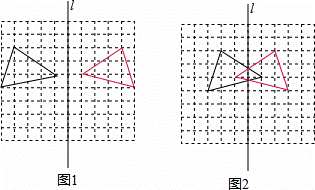
点评:本题主要考查了利用轴对称变换作图,根据网格特点,找出三角形关于直线l的对称点是解题的关键.
考点:作图—复杂作图。
专题:作图题。
分析:设正方形的面积为2,则△BEC的面积为1,根据题意,分成的每一个直角梯形的面积为![]() ,然后找出正方形的中心O,过中心O分别作OF∥AD交AB于点F、作OG∥CD交BE于点H,交BC边于点G,连接OD、HE,即可作出.
,然后找出正方形的中心O,过中心O分别作OF∥AD交AB于点F、作OG∥CD交BE于点H,交BC边于点G,连接OD、HE,即可作出.
解答:解:如图所示,①②③④部分就是全等的直角梯形.
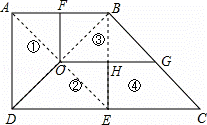
点评:本题主要考查了复杂作图,根据面积确定出从正方形的中心入手求解是解题的关键,难度中等,但不容易考虑.
已知α是锐角,且点A(,a),B(sin2α+cos2α,b), C(-m+2m-2,c)都在二次函数y=-x+x+3的图象上,那么a、b、c的大小关系是 ( )
(本题主要考查二次函数的性质,增减性和三角函数求值)
A.a<b<c B.a<c<b C.b<c<a D.c<b<a
某企业为了改善污水处理条件,决定购买A、B两种型号的污水处理设备共8台,其中每台的价格、月处理污水量如下表:
|
|
A型 |
B型 |
|
价 格(万元/台) |
8 |
6 |
|
月处理污水量(吨/月) |
200 |
180 |
经预算,企业最多支出57万元购买污水处理设备,且要求设备月处理污水量不低于1490吨.
(1)企业有哪几种购买方案?
(2)哪种购买方案更省钱?
【解析】本题主要考查对于一元一次不等式组的应用,要注意本题中有两个解
如图,AB是圆O的直径,作半径OA的垂直平分线,交圆O于C、D两点,垂足为H,联结BC、BD.

(1)求证:BC=BD;
(2)已知CD=6,求圆O的半径长.
【解析】本题主要考查全等三角形的判定勾股定理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com