练习册

  • 练习册
  • 试题
    从的过程中s随t变化的规律是: . 【查看更多】

     

    题目列表(包括答案和解析)

    在“探究小车速度随时间变化的规律”实验中得到的一条纸带，从O点开始每5个点取一个测量点，分别为A、B、C、D、E、F，各点间距如图：
    ①根据
    匀变速直线运动中中间时刻的瞬时速度等于该过程中的平均速度
    匀变速直线运动中中间时刻的瞬时速度等于该过程中的平均速度
    计算各点的瞬时速度，可得：vA=
    0.161
    0.161
    m/s，vB=
    0.239
    0.239
    m/s，vC=
    0.320
    0.320
    m/s，vD=
    0.401
    0.401
    m/s，vE=
    0.479
    0.479
    m/s．
    ②在右边所示坐标中作出小车的v-t图象，根据图线求出加速度a=
    0.80
    0.80
    m/s2
    ③将图线延长与纵轴相交，交点的速度是
    0.800
    0.800
    m/s，此速度的物理意义是
    O点速度
    O点速度

    ④根据
    速度v与时间t的图象是一条倾斜的直线
    速度v与时间t的图象是一条倾斜的直线
    ，可判定小车做
    匀加速直线
    匀加速直线
    运动．

    查看答案和解析>>

     在“探究小车速度随时间变化的规律”的实验中，

    （1）需要的器材有： 电磁打点计时器、（长木板、）复写纸片、导线、        、        、     

    （2）下列说法正确的是

    A．拖动纸带的同时，闭合电源开关

    B．先闭合电源开关，让打点计时器正常工作时，拖动纸带

    C．纸带上的打点密集说明，纸带运动速度较大

    D．利用打出的纸带可以十分准确的求出打下某些点时纸带运动的瞬时速度

    （3）某同学拖动纸带运动，打点计时器在纸带上打出一系列点，电源的频率是50Hz，处理时每隔1个点取一个记数点,标上字母A、B、C、D、E、F，A点与0刻度对齐。

    如图所示，某同学用mm刻度尺进行测量，请帮忙读出B、C在刻度尺上的位置，填到下表中:

    计数点

    B

    C

    D

    E

    F

    位置（cm）

    4.44

    6.22

    8.12

    由读出数据可计算出打下AF段纸带时小车的平均速度为       m/s。

    （4）若认为一段时间中间时刻的瞬时速度就是这段时间内的平均速度，则打点计时器打下C点时小车的速度VC =       m/s，小车从C点运动D点过程中的加速度a=          m/s2。

    （5）在右边所给坐标纸上建好坐标，作出纸带运动的打下B至E点的速度-时间图像（即v-t图像）(从打下A点开始计时)。

    查看答案和解析>>

    在“探究小车速度随时间变化规律”的实验中，某同学测量数据后，通过计算到了小车运动过程中各计时时刻的速度如表格所示：
    位置编号 0 1 2 3 4 5
    时间t/s 0 0.1 0.2 0.3 0.4 0.5
    速度v/m?s-1 0.38 0.63 0.88 1.12 1.38 1.63
    因此次实验的原始纸带没有保存，另一同学想估算小车从位置0到位置5的位移，其所用方法是将每个0.1s视为匀速运动，然后估算如下：
    x=（0.38×0.1+0.63×0.1+0.88×0.1+1.12×0.1+1.38×0.1）那么，该同学得到的位移
    小于
    小于
    ．（选填“大于”、“等于”或“小于”）实际位移，为了使计算位移的误差尽可能小，你认为采取什么方法更合适，为什么？（不必算出具体数据）
    可以先计算相邻位置间的平均速度，再得到位移，这是因为表中每隔0.1s的速度增加在误差范围内相同，即为匀变速直线运动，平均速度可以由公式
    .
    v
    =
    v1+v2
    2
    求出，还可以求出加速度，应用匀变速直线运动公式x=v0t+
    1
    2
    at2    得出位移．
    可以先计算相邻位置间的平均速度，再得到位移，这是因为表中每隔0.1s的速度增加在误差范围内相同，即为匀变速直线运动，平均速度可以由公式
    .
    v
    =
    v1+v2
    2
    求出，还可以求出加速度，应用匀变速直线运动公式x=v0t+
    1
    2
    at2    得出位移．
    ．

    查看答案和解析>>

    要“探究小车速度随时间变化规律”的实验中，某同学测量数据后，通过计算到了小车运动过程中各计时时刻的速度如表格所示：

    位置编号

    0

    1

    2

    3

    4

    5

    时间t/s

    0

    0.1

    0.2

    0.3

    0.4

    0.5

    速度v/m?s-1

    0.38

    0.63

    0.88

    1.12

    1.38

    1.63

    因此次实验的原始纸带没有保存，另一同学想估算小车从位置0到位置5的位移，其所用方法是将每个0.1s视为匀速运动，然后估算如下：

    x=（0.38×0.1+0.63×0.1+0.88×0.1+1.12×0.1+1.38×0.1）m=

    那么，该同学得到的位移              （选填“大于”、“等于”或“小于”）实际位移，为了使计算位移的误差尽可能小，你认为采取什么方法更合适，为什么？（不必算出具体数据）

    查看答案和解析>>

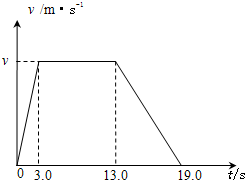    物理兴趣小组活动中，小红提出如下问题：“电梯上升过程中有什么运动规律？”小明同学决定通过实验来探究这一问题．
    小明选择了台秤、钩码和停表等仪器进行实验，经过多次仔细的观察和测量，他探究出了电梯上升过程中速度随时间的变化规律（v-t图象），如图所示．
    下面是小明的某次实验情况：他将台秤水平放置在电梯内，并把一质量m=0.5kg的钩码放在台秤的托盘上，电梯从第一层开始启动经过不间断地运行，最后停在最高层．在整个过程中，他记录下了台秤在不同时间段内的示数，记录的数据如下表所示，但由于疏忽，小明没有记录下13.0～19.0s 时间段内台秤的示数．请通过分析或计算解答下列问题：（设在每个时间段内台秤的示数都是稳定的，重力加速度g取10m/s2．）
    （1）请你根据v-t图象及表格中的数据，判断在0～3.0s、3.0～13.0s、13.0～19.0s时间段内，电梯内的钩码所处的超、失重状态，并将判断的结果填入表格内相应的位置．
    （2）在0～3.0s内，钩码的加速度大小是多少？
    （3）v-t图象中电梯做匀速运动时的速度v是多少？
    （4）电梯在13.0～19.0s 时间段内台秤的示数应该是多少？
    时间（s） 台秤示数（N） 钩码超、失重判断
    电梯启动前 5.0
    0～3.0 5.8
    3.0～13.0 5.0
    13.0～19.0 ？
    19.0以后 5.0

    查看答案和解析>>

    一、填空题，每小题4分，共20分

    1、光子；科学假说；        2、；      3、TB=TC<TD；θB=θC>θD；

    4、E1>E2；△E1 = △E2；     5、5，30

    二、选择题：共40分。

    说明

    Ⅰ单项选择题（每题4分）

    Ⅱ多项选择题（每题5分）

    题号

    6

    7

    8

    9

    10

    11

    12

    13

    14

    选项

    C

    D

    B

    A

    A

    AB

    BD

    AD

    CD

    三、实验题：共30分

    15、A

    16、(1)A；(2)一节干电池、保护电阻 ；将电池与电流表、保护电阻串接

    17、(1) ① ③ ；  ①中有导电物质的一面朝上，③中应使用电压传感器；(2) a ；(3) f ，向右

    18、（1）作图法 ；（2）画出的s-t图（如图线甲）和的s-t图（如图线乙）                                                          

     

    在误差允许的范围内，图线甲为直线，物体从A到B的运动为匀速直线运动，从图线的斜率可求得： ，     

    从乙图中无法直接判断s、t之间的关系，但是该图线接近于二次函数的图像。为了验证这个猜想，通过转换变量来进行，即作s-t2图线，为此求得表格如下：

    时间t(s)

    0.89

    1.24

    1.52

    1.76

    1.97

    新变量t2(s2)

    0.79

    1.54

    2.31

    3.10

    3.88

    位移s(m)

    0.25

    0.50

    0.75

    1.00

    1.25

     

    依据上表中的t2、、s数据可作图线丙。从图像中看出s与t2、呈线性变化关系，由图中斜率求得，即故

    （3）从的过程中s随t变化的规律是： 物体作匀速直线运动，          

    从的过程中s随t变化的规律是：物体作初速度为零的匀加速直线运动，

     

    19、解：（1）由图线可看出滑块上升和下滑的加速度大小几乎相等，说明摩擦力对滑块Ａ运动的影响可以忽略。

    （2）因为有滑动摩擦力，所以图线不对称。

     

    上滑时，s1 =1/2 g(sinθ+μcosθ)t12

    下滑时，s 2=1/2 g(sinθ-μcosθ)t22

    代入图给数据s1 = s2=0.55m   t1=0.4s  t2=0.6s

     2

    解得sinθ=0.5  θ＝30°  μ=0.22

     (θ角在arcsin0.45 ―arcsin0.55范围都算对；μ在0.2―0.3都算对)

     

    四、计算题：共60分

    20、解： 以密闭容器内的一定量气体为研究对象，选取标准状况为该气体的一个已知状态，根据理想气体状态方程可求解.

           取1摩尔气体作为研究对象，在标准状态下为，所包含的分子数为NA=6.023×1023个.在题设条件下，设其体积为V，则根据气态方程：

           有

           每个分子所占的空间体积为，分子间的距离为

    21、解：该同学的解法不合理。（1分）

    因为在施加竖直向下的电场后，物体对桌面压力N=mg+qE，因而物体受到的滑动摩擦力f=mN=m(mg+qE)，而这位同学仍用f=mmg来计算摩擦力做的功。（2分）

    正确解答：

    未加电场：mg（H-h）-mmgSAC=0                                      （1分）

    加电场后：（mg+qE）（H-h）-m（mg+qE）SAC=    （2分）

    [ 联解上述两式得：   u=u0=4米/秒]

    运用平抛运动的公式：       （2分）

     得：S==4                   （2分）

    22、、解：由闭合电路欧姆定律作aP两端的Uap―I图像，因图上任意一点的Uap与I所对应的矩形面积是外电路电阻Rx的输出功率，从而由已知Rx的功率求出对应的Rx值。

    根据闭合电路欧姆定律

    作图像如图所示，由图可分析找到滑动变阻器的发热功率为9W的A点和B点，所以Rx有两个值。

     

    23、解：(1)输电线冰层体积V冰=πR2L，由于对称性塔尖上所受压力的增加量等于一根输电线上冰层的重力，即ΔN=ρgV冰=ρgπR2L。

        (2)输电线与冰层的总质量为：M=m0L+ρπR2L，输电线受到三个力作用，由共点力平衡条件得：

        2F1cosθ=m0gL+ρgπR2L   

    最高点所受拉力为：

        由半根输电线的受力可得最低点的拉力为

       

        (3)设铁塔被冰包裹时的质量为m`，则

      

        铁塔即将翻倒时受到重力、地面拉力和输电线拉力作用，以―端为轴，R取最大值时有：

          

      

    24、解：（1）由题意知圆环所在处在磁感应强度B为：   ……①

    圆环的有效切割长度为其周长即： ……②

    圆环的电阻R电为：……③

    当环速度为v时，切割磁感线产生的电动势为：……④

    电流为：     ……⑤

    故圆环速度为v时电功率为：P=I2R电……⑥

    联立以上各式解得：……⑦

    （2）当圆环加速度为零时，有最大速度vm

    此时……⑧    由平衡条件……⑨

    ……⑩       联立⑧⑨⑩解得……⑾

    （3）由能量守恒定律……⑿

    解得……⒀

    评分标准：③④⑤⑧⑨⑾⒀各2分，⑥⑦⑩各1分，⑿3分共20分

     

     

     

     

     

     

     

     

     


    同步练习册答案