
题目列表(包括答案和解析)
 如题13(a)图,质量为M的滑块A放在气垫导轨B上,C为位移传感器,它能将滑块A到传感器C的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示滑块A的位移-时间(s-t)图象和速率-时间(v-t)图象。整个装置置于高度可调节的斜面上,斜面的长度为了
如题13(a)图,质量为M的滑块A放在气垫导轨B上,C为位移传感器,它能将滑块A到传感器C的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示滑块A的位移-时间(s-t)图象和速率-时间(v-t)图象。整个装置置于高度可调节的斜面上,斜面的长度为了![]() 、高度为
、高度为![]() 。(取重力加速度g=9.8m/s2,结果可保留一位有效数字)
。(取重力加速度g=9.8m/s2,结果可保留一位有效数字)
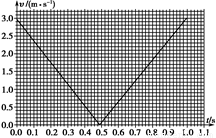
(1)现给滑块A一沿气垫导轨向上的初速度,A的v-t图线如题13(b)图所示。从图线可得滑块A下滑时的加速度 a= m/s2 ,摩擦力对滑块A运动的影响 。(填“明显,不可忽略”或“不明显,可忽略”)
(2)此装置还可用来验证牛顿第二定律。实验时通过改变 ,可验证质量一定时,加速度与力成正比的关系;实验时通过改变 ,可验证力一定时,加速度与质量成反比的关系。
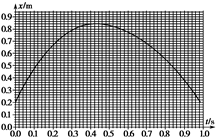
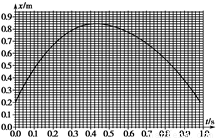
(3)将气垫导轨换成滑板,滑块A换成滑块A’,给滑块A’一沿滑板向上的初速度,A’的s-t图线如题13(c)图。图线不对称是由于 造成的,通过图线可求得滑板的倾角θ= (用反三角函数表示),滑块与滑板间的动摩擦因数μ=


(12分)如图所示,质量为M的滑块A放在气垫导轨B上,C为位移传感器,它能将滑块A到传感器C的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示滑块A的位移—时间(x-t)图象和速率—时间(v-t)图象.整个装置置于高度可调节的斜面上,斜面的长度为l、高度为h.(取重力加速度g="9.8" m/s2,结果保留一位有效数字).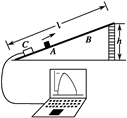
(1)现给滑块A一沿气垫导轨向上的初速度,A的v-t图线如下图实所示.从图线可得滑块A下滑时的加速度a = m/s2,摩擦力对滑块A运动的影响 .(填“明显,不可忽略”或“不明显,可忽略”)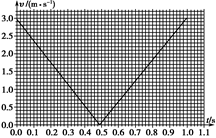
(2)此装置还可用来验证牛顿第二定律.实验时通过改变 可验证质量一定时,加速度与力成正比的关系;通过改变 可验证力一定时,加速度与质量成反比的关系.
(3)将气垫导轨换成滑板,滑块A换成滑块A′,给滑块A′一沿滑板向上的初速度,A′的x-t图线如下图实所示.图线不对称是由于 造成的,通过图线可求得滑块与滑板间的动摩擦因数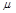 = .
= .

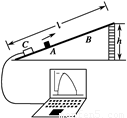
题13(a)图
(1)现给滑块A 一沿气垫导轨向上的初速度,A的v-t图线如题13(b)图所示.从力线可得滑块A下滑时的加速度a= m/s2,摩擦力对滑块A运动的影响 .(填“明显,不可忽略”或“不明显,可忽略”)
(2)此装置还可用来验证牛顿第二定律.实验时通过改变 ,可验证质量一定时,加速度与力成正比关系;通过改变 ,可验证力一定时,加速度与质量成反比的关系.
(3)将气垫导轨换成滑板,滑块A换成滑块A′,给滑块A′一沿滑板向上的初速度,A′的s-t图线如题13(c)图.图线不对称是由于 造成的,通过图线可求得滑板的倾角![]() = (用反三角函数表示),滑块与滑板间的动摩擦因数
= (用反三角函数表示),滑块与滑板间的动摩擦因数![]() = .
= .

题13(b)图

题13(c)图
(12分)如图所示,质量为M的滑块A放在气垫导轨B上,C为位移传感器,它能将滑块A到传感器C的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示滑块A的位移—时间(x-t)图象和速率—时间(v-t)图象.整个装置置于高度可调节的斜面上,斜面的长度为l、高度为h.(取重力加速度g="9.8" m/s2,结果保留一位有效数字).
(1)现给滑块A一沿气垫导轨向上的初速度,A的v-t图线如下图实所示.从图线可得滑块A下滑时的加速度a = m/s2,摩擦力对滑块A运动的影响 .(填“明显,不可忽略”或“不明显,可忽略”)
(2)此装置还可用来验证牛顿第二定律.实验时通过改变 可验证质量一定时,加速度与力成正比的关系;通过改变 可验证力一定时,加速度与质量成反比的关系.
(3)将气垫导轨换成滑板,滑块A换成滑块A′,给滑块A′一沿滑板向上的初速度,A′的x-t图线如下图实所示.图线不对称是由于 造成的,通过图线可求得滑块与滑板间的动摩擦因数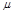 = .
= .
一、填空题,每小题4分,共20分
1、光子;科学假说; 2、 ;
3、TB=TC<TD;θB=θC>θD;
;
3、TB=TC<TD;θB=θC>θD;
4、E1>E2;△E1 = △E2; 5、5,30
二、选择题:共40分。
说明
Ⅰ单项选择题(每题4分)
Ⅱ多项选择题(每题5分)
题号
6
7
8
9
10
11
12
13
14
选项
C
D
B
A
A
AB
BD
AD
CD
三、实验题:共30分
15、A
16、(1)A;(2)一节干电池、保护电阻 ;将电池与电流表、保护电阻串接
17、(1) ① ③ ; ①中有导电物质的一面朝上,③中应使用电压传感器;(2) a ;(3) f ,向右
18、(1)作图法 ;(2)画出 的s-t图(如图线甲)和
的s-t图(如图线甲)和 的s-t图(如图线乙)
的s-t图(如图线乙)
 在误差允许的范围内,图线甲为直线,物体从A到B的运动为匀速直线运动,从图线的斜率可求得:
在误差允许的范围内,图线甲为直线,物体从A到B的运动为匀速直线运动,从图线的斜率可求得: ,
, 
从乙图中无法直接判断s、t之间的关系,但是该图线接近于二次函数的图像。为了验证这个猜想,通过转换变量来进行,即作s-t2图线,为此求得表格如下:

时间t(s)
0.89
1.24
1.52
1.76
1.97
新变量t2(s2)
0.79
1.54
2.31
3.10
3.88
位移s(m)
0.25
0.50
0.75
1.00
1.25
依据上表中的t2、、s数据可作图线丙。从图像中看出s与t2、呈线性变化关系,由图中斜率求得,即 故
故
(3)从 的过程中s随t变化的规律是: 物体作匀速直线运动,
的过程中s随t变化的规律是: 物体作匀速直线运动,
从 的过程中s随t变化的规律是:物体作初速度为零的匀加速直线运动,
的过程中s随t变化的规律是:物体作初速度为零的匀加速直线运动,
19、解:(1)由图线可看出滑块上升和下滑的加速度大小几乎相等,说明摩擦力对滑块A运动的影响可以忽略。

(2)因为有滑动摩擦力,所以图线不对称。
上滑时,s1 =1/2 g(sinθ+μcosθ)t12
下滑时,s 2=1/2 g(sinθ-μcosθ)t22
代入图给数据s1 = s2=
2
解得sinθ=0.5 θ=30° μ=0.22
(θ角在arcsin0.45 ―arcsin0.55范围都算对;μ在0.2―0.3都算对)
四、计算题:共60分
20、解: 以密闭容器内的一定量气体为研究对象,选取标准状况为该气体的一个已知状态,根据理想气体状态方程可求解.
取1摩尔气体作为研究对象,在标准状态下为 ,所包含的分子数为NA=6.023×1023个.在题设条件下,设其体积为V,则根据气态方程:
,所包含的分子数为NA=6.023×1023个.在题设条件下,设其体积为V,则根据气态方程:
有
每个分子所占的空间体积为 ,分子间的距离为
,分子间的距离为
21、解:该同学的解法不合理。(1分)
因为在施加竖直向下的电场后,物体对桌面压力N=mg+qE,因而物体受到的滑动摩擦力f=mN=m(mg+qE),而这位同学仍用f=mmg来计算摩擦力做的功。(2分)
正确解答:
未加电场:mg(H-h)-mmgSAC=0 (1分)
加电场后:(mg+qE)(H-h)-m(mg+qE)SAC= (2分)
(2分)
[ 联解上述两式得:
u=u0=
运用平抛运动的公式: (2分)
(2分)
得:S= =4
=4 (2分)
(2分)
22、、解:由闭合电路欧姆定律作aP两端的Uap―I图像,因图上任意一点的Uap与I所对应的矩形面积是外电路电阻Rx的输出功率,从而由已知Rx的功率求出对应的Rx值。
根据闭合电路欧姆定律


作 图像如图所示,由图可分析找到滑动变阻器的发热功率为9W的A点和B点,所以Rx有两个值。
图像如图所示,由图可分析找到滑动变阻器的发热功率为9W的A点和B点,所以Rx有两个值。

23、解:(1)输电线冰层体积V冰=πR
(2)输电线与冰层的总质量为:M=m
最高点所受拉力为:
由半根输电线的受力可得最低点的拉力为

(3)设铁塔被冰包裹时的质量为m`,则

铁塔即将翻倒时受到重力、地面拉力和输电线拉力作用,以―端为轴,R取最大值时有:

24、解:(1)由题意知圆环所在处在磁感应强度B为:  ……①
……①
圆环的有效切割长度为其周长即:  ……②
……②
圆环的电阻R电为: ……③
……③
当环速度为v时,切割磁感线产生的电动势为: ……④
……④
电流为:  ……⑤
……⑤
故圆环速度为v时电功率为:P=I2R电……⑥
联立以上各式解得: ……⑦
……⑦
(2)当圆环加速度为零时,有最大速度vm
此时 ……⑧ 由平衡条件
……⑧ 由平衡条件 ……⑨
……⑨
 ……⑩ 联立⑧⑨⑩解得
……⑩ 联立⑧⑨⑩解得 ……⑾
……⑾
(3)由能量守恒定律 ……⑿
……⑿
解得 ……⒀
……⒀
评分标准:③④⑤⑧⑨⑾⒀各2分,⑥⑦⑩各1分,⑿3分共20分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com