
题目列表(包括答案和解析)
.航模兴趣小组设计出一架遥控飞行器,其质量m=2 kg,动力系统提供的恒定升力F=28 N.试飞时,飞行器从地面由静止开始竖直上升.设飞行器飞行时所受的空气阻力恒为f=4 N,g取10 m/s2.
(1)第一次试飞,飞行器飞行t1=8 s时到达高度H等于多少?
(2)第二次试飞,飞行器飞行t2=6 s时遥控器出现故障,飞行器立即失去升力,求飞行器减速上升阶段的加速度的大小.
【解析】:(1)第一次飞行中,设加速度为a1,
由牛顿第二定律得F-mg-f=ma1
飞行器上升的高度H=a1t
解得H=64 m.
(2)第二次飞行中,设失去升力后的加速度为a2,
由牛顿第二定律得-(mg+f)=ma2
解得a2=-12 m/s2.
.航模兴趣小组设计出一架遥控飞行器,其质量m=2 kg,动力系统提供的恒定升力F=28 N.试飞时,飞行器从地面由静止开始竖直上升.设飞行器飞行时所受的空气阻力恒为f=4 N,g取10 m/s2.
(1)第一次试飞,飞行器飞行t1=8s时到达高度H等于多少?
(2)第二次试飞,飞行器飞行t2=6s时遥控器出现故障,飞行器立即失去升力,求飞行器减速上升阶段的加速度的大小.
【解析】:(1)第一次飞行中,设加速度为a1,
由牛顿第二定律得F-mg-f=ma1
飞行器上升的高度H=a1t
解得H=64m.
(2)第二次飞行中,设失去升力后的加速度为a2,
由牛顿第二定律得-(mg+f)=ma2
解得a2=-12 m/s2.
如图为一空间探测器的示意图,P1、P2、P3、P4是四个喷气发动机,P1、P3的连线与空间一固定坐标系的x轴平行,P2、P4的连线与y轴平行.每台发动机喷气时,都能向探测器提供推力,但不会使探测器转动,开始时,探测器相对于坐标系以恒定的速率v0沿正x方向平动.先开动P1,使P1在极短时间内一次性喷出质量为m的气体,气体喷出时相对于坐标系的速度大小为v.然后开动P2,使P2在极短的时间内一次性喷出质量为m的气体,气体喷出时相对坐标系的速度大小为v.此时探测器的速度大小为2v0,且方向沿正y方向.假设探测器的总质量为M(包括气体的质量),求每次喷出气体的质量m与探测器总质量M的比值和每次喷出气体的速度v与v0的比值.
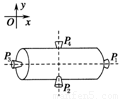
【解析】:探测器第一次喷出气体时,沿x方向动量守恒,且探测器速度变为零.
即Mv0=mv①
第二次喷出气体时,沿y方向动量守恒:
0=(M-2m)·2v0-mv②
解①②得:=,=
如图为一空间探测器的示意图,P1、P2、P3、P4是四个喷气发动机,P1、P3的连线与空间一固定坐标系的x轴平行,P2、P4的连线与y轴平行.每台发动机喷气时,都能向探测器提供推力,但不会使探测器转动,开始时,探测器相对于坐标系以恒定的速率v0沿正x方向平动.先开动P1,使P1在极短时间内一次性喷出质量为m的气体,气体喷出时相对于坐标系的速度大小为v.然后开动P2,使P2在极短的时间内一次性喷出质量为m的气体,气体喷出时相对坐标系的速度大小为v.此时探测器的速度大小为2v0,且方向沿正y方向.假设探测器的总质量为M(包括气体的质量),求每次喷出气体的质量m与探测器总质量M的比值和每次喷出气体的速度v与v0的比值.
【解析】:探测器第一次喷出气体时,沿x方向动量守恒,且探测器速度变为零.
即Mv0=mv①
第二次喷出气体时,沿y方向动量守恒:
0=(M-2m)·2v0-mv②
解①②得:=,=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com