一个光滑圆环固定在竖直平面内，环上套着两个小球A和B（中央有孔），A、B间由细线连接着，它们处于如图中所示位置时恰好都能保持静止状态。此情况下，B球与环中心O处于同一水平面上，AB间的细绳呈伸直状态，与水平线成30⁰夹角。已知B球的质量为m，求：【小题1】细绳对B球的拉力和A球的质量；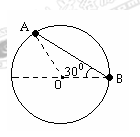

【小题2】若剪断细线瞬间A球的加速度；
【小题3】剪断细线后，B球第一次过圆环最低点时对圆环的压力。

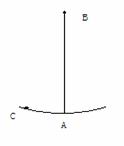
如图，A为半径为R的光滑圆轨道的最低点，B、C为两个完全相同的小球(均可看成质点)，将B球放在A的正上方高度为h处，将C球放在离A很近的轨道上，让B、C球同时由静止开始运动(不计空气阻力)，设C球第一次到达A点时与B球相遇。则h与R的应满足什么关系？

如图2所示,两根平行的金属导轨，固定在同一水平面上，磁感应强度B=0.05 T的匀强磁场与导轨所在平面垂直(图中未画出)，导轨的电阻很小，可忽略不计.导轨间的距离l=0.20 m.两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆的电阻均为R=0.50 Ω.在t=0时刻，两杆都处于静止状态.现有一与导轨平行、大小为0.20 N的恒力F作用于金属杆甲上，使金属杆在导轨上滑动.经过t=5.0 s，金属杆甲的加速度为a=1.37 m/s².问此时两金属杆的速度各为多少？?

图2

【解析】设t=5.0 s时两金属杆甲、乙之间的距离为x,速度分别为v₁和v₂,经过很短的时间Δt,杆甲移动距离v₁Δt,杆乙移动距离v₂Δt,回路面积改变ΔS=［(x-v₂Δt)+v₁Δt］l-lx=(v₁-v₂)lΔt.由法拉第电磁感应定律知,回路中的感应电动势回路中的电流

对杆甲由牛顿第二定律有F-BlI=ma

由于作用于杆甲和杆乙的安培力总是大小相等、方向相反,所以t=5.0 s时两杆的动量(t=0时为0)等于外力F的冲量Ft=mv₁+mv₂

联立以上各式解得

代入数据得v₁=8.15 m/s,v₂=1.85 m/s.

如图2所示,两根平行的金属导轨，固定在同一水平面上，磁感应强度B=0.05 T的匀强磁场与导轨所在平面垂直(图中未画出)，导轨的电阻很小，可忽略不计.导轨间的距离l=0.20 m.两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆的电阻均为R=0.50 Ω.在t=0时刻，两杆都处于静止状态.现有一与导轨平行、大小为0.20 N的恒力F作用于金属杆甲上，使金属杆在导轨上滑动.经过t=5.0 s，金属杆甲的加速度为a=1.37 m/s².问此时两金属杆的速度各为多少？?

图2

【解析】设t=5.0 s时两金属杆甲、乙之间的距离为x,速度分别为v₁和v₂,经过很短的时间Δt,杆甲移动距离v₁Δt,杆乙移动距离v₂Δt,回路面积改变ΔS=［(x-v₂Δt)+v₁Δt］l-lx=(v₁-v₂)lΔt.由法拉第电磁感应定律知,回路中的感应电动势回路中的电流

对杆甲由牛顿第二定律有F-BlI=ma

由于作用于杆甲和杆乙的安培力总是大小相等、方向相反,所以t=5.0 s时两杆的动量(t=0时为0)等于外力F的冲量Ft=mv₁+mv₂

联立以上各式解得

代入数据得v₁=8.15 m/s,v₂=1.85 m/s.

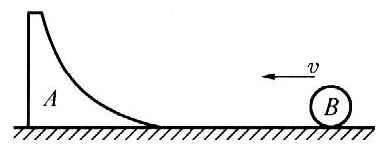
如图所示,木块A的右侧为光滑曲面,且下端极薄,其质量为2.0㎏,静止于光滑水平面上,一质量为2.0㎏的小球B以2.0m/s的速度从右向左运动冲上A的曲面,与A发生相互作用.【6】

(1)B球沿A曲面上升的最大高度(设B球不能飞出去)是(        ).【2】

(A)0.40m                        (B)0.20m        

(C)0.10m                        (D)0.05m

(2)B球沿A曲面上升到最大高度处时的速度是(        ).【2】

(A)0                                (B)1.0m/s                (C)0.71m/s                (D)0.50m/s

(3)B球与A曲面相互作用结束后,B球的速度是(        ).【2】

(A)0                                (B)1.0m/s                (C)0.71m/s                (D)0.50m/s