
题目列表(包括答案和解析)
| ax+1 |
| 3x-1 |
| Sn |
| Tn |
| an |
| bn |
| 5 |
| 2 |
| 5 |
| 2 |
| x |
| x+1 |
| 1 | ||
|
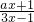 ,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且
,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且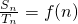 (n∈N+).
(n∈N+). ,求g(n)的最大值;
,求g(n)的最大值; ,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由. ,数列{bn}的公差为3,且dn=bn-(n-1),h(x)=
,数列{bn}的公差为3,且dn=bn-(n-1),h(x)= .试证明:h(d1)•h(d2)…h(dn)<
.试证明:h(d1)•h(d2)…h(dn)<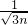 .
.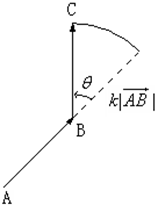 如图,
如图, 的大小是
的大小是 大小的k倍,
大小的k倍, 的方向由
的方向由 的方向逆时针旋转θ角得到,则我们称
的方向逆时针旋转θ角得到,则我们称 经过一次(θ,k)延伸得到
经过一次(θ,k)延伸得到 . 已知
. 已知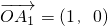
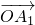 经过2次
经过2次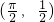 延伸,分别得到向量
延伸,分别得到向量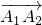 、
、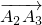 ,求
,求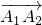 、
、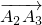 的坐标.
的坐标.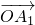 经过n-1次
经过n-1次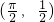 延伸得到的最后一个向量
延伸得到的最后一个向量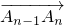 ,(n∈N*,n>1),设点An(xn,yn),求An的极限位置
,(n∈N*,n>1),设点An(xn,yn),求An的极限位置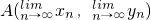
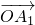 经过2次(θ,k)延伸得到向量
经过2次(θ,k)延伸得到向量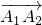 、
、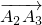 ,其中k>0,θ∈(0,π),若
,其中k>0,θ∈(0,π),若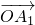 、
、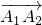 、
、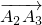 恰能够构成一个三角形(即A3与O重合),求θ,k的值.
恰能够构成一个三角形(即A3与O重合),求θ,k的值. ,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且
,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且 (n∈N+).
(n∈N+). ,求g(n)的最大值;
,求g(n)的最大值; ,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由. ,数列{bn}的公差为3,且dn=bn-(n-1),h(x)=
,数列{bn}的公差为3,且dn=bn-(n-1),h(x)= .试证明:h(d1)•h(d2)…h(dn)<
.试证明:h(d1)•h(d2)…h(dn)< .
. (2013•松江区二模)如图所示,向量
(2013•松江区二模)如图所示,向量| BC |
| AB |
| AB |
| BC |
| AB |
| BC |
| OA1 |
| OA1 |
| 1 |
| 2 |
| 2π |
| 3 |
| An-1An |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com