题目列表(包括答案和解析)
（09年深圳教苑中学月考）（17分）如图所示，一质量为M，长为l的长方形木板B放在光滑水平地面上，在其右端放一质量为
的小木块A，
。现以地面为参照系，给A、B以大小相等、方向相反的初速度，使A开始向左运动、B开始向右运动，但最后A刚好没有滑离B板，以地面为参照系。
（1）若已知A和B的初速度大小
，求它们最后的速度的大小和方向；
（2）若初速度大小未知，求小木块A向左运动到达的最远处（从地面上看）离出发点的最大距离。
（09年深圳教苑中学月考）(14分)2005年lO月12日，我国成功地发射了“神舟”六号载人宇宙飞 船，飞船进入轨道运行若干圈后成功实施变轨进入圆轨道运行。经过了近5天的运行后，飞船的返回舱顺利降落在预定地点。设“神舟”六号载人飞船在圆轨道上绕地球运行n圈所用的时间为t，若地球表面的重力加速度为g，地球半径为R，求：
(1)飞船的圆轨道离地面的高度；
(2)飞船在圆轨道上运行的速率。
（09年深圳教苑中学月考）(14分)如图所示(a)，一条长为3L的绝缘丝线穿过两个质量都是m的小金属环A和B，将丝线的两端共同系于天花板上的O点，使金属环带电后，便因排斥而使丝线构成一个等边三角形，此时两环恰处于同一水平线上，若不计环与线间的摩擦，求金属环所带电量是多少？某同学在解答这道题时的过程如下：
设电量为q，小环受到三个力的作用，拉力T、重力mg和库仑力F，受力分析如图b，由受力平衡知识得，
=mgtan30°，
。
你认为他的解答是否正确？如果不正确，请给出你的解答？
（09年深圳教苑中学月考）(12分)某同学设计了一个探究加速度与物体所受合力F及质量m的关系实验。如图(a)为实验装置简图，A为小车，B为打点计时器，C为装有砂的砂桶，D为一端带有定滑轮的长方形木板，实验中认为细绳对小车拉力F等于砂和砂桶总重量，小车运动加速度a可用纸带上点求得：
(1)图(b)为某次实验得到的纸带(交流电的频率为50Hz)，试由图中数据求出小车加速度值；
(2)保持砂和砂桶质量不变，改变小车质量m，分别得到小车加速度a与质量m及对应的
数据如下表：
根据上表数据，为直观反映：F不变时，a与m的关系，请在方格坐标纸中选择恰当物理量，建立坐标系，并作出图线.从图线中得到：F不变时，小车加速度a与质量之间定量关系式是_____________.
(3)保持小车质量不变，改变砂和砂桶重量，该同学根据实验数据作出了加速度a与合力F图线，如图(d)所示，该图线不通过原点，明显超出偶然误差范围，其主要原因是_______________________________________________.
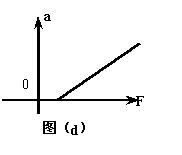
（09年深圳教苑中学月考）（12分）用如图甲所示的装置，来验证碰撞过程中的动量守恒。图中PQ是斜槽，QR为水平槽。O点是水平槽末端R在记录纸上的垂直投影点，A、B两球的质量之比mA:mB＝3:1。先使A球从斜槽上固定位置G由静止释放，在水平地面的记录纸上留下落点痕迹，重复10次，得到10个落点。再把B球放在水平槽上的末端R处，让A球仍从位置G由静止释放，与B球碰撞，碰后A、B球分别在记录纸上留下各自的落点痕迹，重复10次。A、B两球在记录纸上留下的落点痕迹如图乙所示，其中米尺的零点与O点对齐。
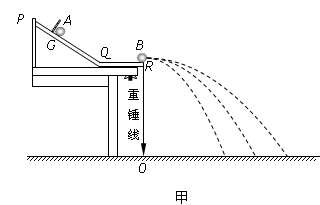
（1）碰撞后A球的水平射程应取_____________cm。
（2）本实验巧妙地利用小球飞行的水平距离表示小球的水平速度。下面的实验条件中，可能不能使小球飞行的水平距离表示为水平速度的是__________________。
A．使A、B两小球的质量之比改变为5:1
B．升高固定点G的位置
C．使A、B两小球的直径之比改变为1:3
D．升高桌面的高度，即升高R点距地面的高度
（3）利用此次实验中测得的数据计算碰撞前的总动量与碰撞后的总动量的比值为 。（结果保留三位有效数字）
一．不定项选择题
1.BCD 2.B 3.AC 4.BC 5.B 6.A
二．实验题
1．
设A物块碰撞B物块前后的速度分别为v1和v2，碰撞过程中动量守恒，
代入数据得： 
（4分）
2.①14.45－14.50（4分）， ②C（4分），③1.01－1.02 。（4分）
三．计算题
1、
解：（1）设A球与B球碰撞前瞬间的速度为v0，
由动能定理得， 
①……………………（2分）
解得：
②
………………………（2分）
碰撞过程中动量守恒
③………………（2分）
机械能无损失，有 
④……………（2分）
解得
负号表示方向向左 ………………（1分）
方向向右 ……………………………（1分）
（2）要使m与M第二次迎面碰撞仍发生在原位置，则必有A球重新回到O处所用的时间t恰好等于B球的
………………………………（1分）
⑥ …………………………………………………………………（1分）
（n=0 、1 、2 、3 ……） ⑦ …………………………（2分）
由题意得： 
⑧ …………………………（1分）
解得： 
（n=0 、1 、2 、3 ……） ⑨ ……………（2分）
2．
解：子弹穿过A时，子弹与A动量守恒，
由动量守恒定律： ……………………… ① 3分
而由 得：v1=300m/s
得： ………………………②
子弹穿过B时， 子弹与B动量守恒，
由动量守恒定律： ………………………③ 3分
又由 …………………④ 2分
得：v2=100m/s
由③，④得： ………………………⑤
子弹穿过B以后，弹簧开始被压缩，A、B和弹簧所组成的系统动量守恒
由动量守恒定律： ………………………⑥ 3分
由能量关系： ……………………⑦ 3分
由② ⑤ ⑥ ⑦得： ………………………⑧ 2分
3.
解(1) 
与
第一次碰撞前，A、B之间的压力等于A的重力，即
…………1分
A对B的摩擦力
…………………………………………1分
而B与地面间的压力等于A、B重力之和，即
…………1分
地面对B的最大静摩擦力 
……………………………….1分
故与第一次碰撞前，B不运动………………………2分
（2）设A第一次碰前速度为v，碰后B的速度为v2
则由动能定理有………………………………………………………………..1分
……………………………………..2分
碰撞过程中动量守恒…………………………………………………………..1分
有 
………………………………………………..2分
解得
………………………………………………….2分
（3）当停止运动时， 继续向右滑行
（
）后停止，设B停止时，的速度为
，则由动能定理……………………………………………………………………1分
得
……………………………………………………..2分
解得
…………………………………………………………………..1分
4．
答案：（1）整个过程中系统克服摩擦力做的总功为
Wf＝µmgl（1＋2＋3＋…＋n）＝
…………………………..2分
整个过程中因碰撞而损失的总动能为
……………………………..1分
（2）设第i次（i≤n－1）碰撞前瞬间，前i个木块粘合在一起的速度为vi，
动能为 
与第i＋１个（i≤n－1）木块碰撞粘合在一起后瞬间的速度为vi＇，
由动量守恒定律 
………………………………………….2分
则
第i次（i≤n－1）碰撞中损失的动能为
…….2分
则第i次（i≤n－1）碰撞中损失的动能与碰撞前动能之比为
（i≤n－1）………………………………………………………1分
（3）n＝４时，共发生了i＝3次碰撞．
第1次碰前瞬间的速度为
，碰撞中动量守恒：
第1次碰后瞬间的速度为
……………………….3分
第2次碰前瞬间的速度为
碰撞中动量守恒：
第2次碰后瞬间的速度为
……………………….3分
第3次碰前瞬间的速度为
碰撞中动量守恒：
第3次碰后瞬间的速度为
………………………...3分
最后滑行到桌边，速度恰好为零，则
……………………….1分
即
整理后得
，代入数据解得
………………………….1分
5.
 |
6．
解：（1）在弹簧弹开的过程中系统动量守恒，假设A运动的方向为正方向，则
Mv1-mv2=0 2分
设从弹开到相遇所需时间为t，则有：
v1t+v2t=2πR 2分
联立以上两式得： 
2分
所以A球转过的角度为θ=120° 2分
（2）以A、B及弹簧组成的系统为研究对象，在弹簧张开的过程中，系统机械能守恒，则有
2分
Mv1-mv2=0 2分
解得： v1=2m/s，v2=4m/s 2分
所以，小球B在运动过程中受到光滑轨道的侧压力是其所需向心力，即：
2分
7．
解：（1）A与B第一次碰撞前，A对B的摩擦力为
2分
地面对B的最大静摩擦力为
2分
故A与B第一次碰撞前，B不运动
2分
（2）设A第一次碰前速度为v，碰后B的速度为v2，则由动能定理有
2分
碰撞过程中动量守恒有
2分
解得 2分
8．
(1)设A与B碰撞前A的速度为 V1 ，碰撞过程动量守恒，有：
mv1=(M+m)v (2分) 代入数据解得：v1=
（2）对A，从开始运动至碰撞B之前，根据动能定理，有：
（2分） 代入数据解得：
9．
（1）设物体从A滑落至B时速率为
(2分)
(1分)
物体与小球相互作用过程中，系统动量守恒，设共同速度为
(2分)
(1分 )
（2）设二者之间的摩擦力为
(2分)
(2分)
得
(1分)
（3）设物体从EF滑下后与车达到相对静止，共同速度为v2相对车滑性的距离为S1，
车停后物体做匀减速运动，相对车滑行距离为S1
(1分)
(1分)
(2分)
联立解得
(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com