
题目列表(包括答案和解析)
5.A解析:因为函数有0,1,2三个零点,可设函数为f(x)=ax(x-1)(x-2)=ax3-3ax2+2ax
因此b=-3a,又因为当x>2时f(x)>0所以a>0,因此b<0
若由一个2*2列联表中的数据计算得k=4.013,那么有 把握认为两个变量有关系.
在数列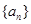 中,
中,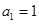 ,当
,当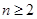 时,
时,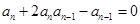
(Ⅰ)求数列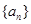 的通项公式;
的通项公式;
(Ⅱ)设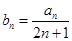 ,求数列
,求数列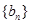 的前
的前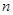 项和
项和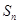 .
.
【解析】本试题主要考查了数列的通项公式的求和 综合运用。第一问中 ,利用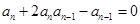 ,得到
,得到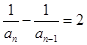 且
且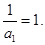 ,故故
,故故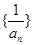 为以1为首项,公差为2的等差数列. 从而
为以1为首项,公差为2的等差数列. 从而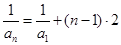

第二问中,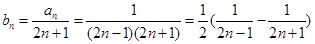
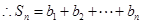
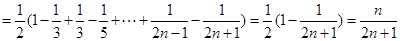
由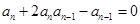 及
及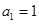 知
知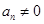 ,从而可得
,从而可得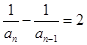 且
且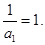
故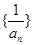 为以1为首项,公差为2的等差数列.
为以1为首项,公差为2的等差数列.
从而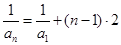
 ……………………6分
……………………6分
(2)
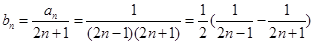 ……………………9分
……………………9分
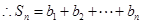
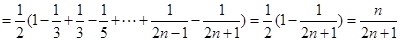
对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时
①求f0(x)和fk(x)的解析式;
②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(2)若Φ(x)=x2,则是否存在正整数k,使得不等式fk(x)<(1-3k)x+4k2+3k-1有解?若存在,求出k的值;若不存在,请说明理由.
对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时
①求f0(x)和fk(x)的解析式;
②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(2)若Φ(x)=x2,则是否存在正整数k,使得不等式fk(x)<(1-3k)x+4k2+3k-1有解?若存在,求出k的值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com