已知函数f(x)=e^x-ax，其中a＞0.

（1）若对一切x∈R，f(x) 1恒成立，求a的取值集合；

（2)在函数f(x)的图像上去定点A（x₁, f(x₁)）,B(x₂, f(x₂))(x₁<x₂)，记直线AB的斜率为k，证明：存在x₀∈（x₁,x₂）,使恒成立.

【解析】解：令.

当时单调递减；当时单调递增，故当时，取最小值

于是对一切恒成立，当且仅当.　　　　　　　　①

令则

当时，单调递增；当时，单调递减.

故当时，取最大值.因此，当且仅当时，①式成立.

综上所述，的取值集合为.

（Ⅱ）由题意知，令则

令，则.当时，单调递减；当时，单调递增.故当，即

从而，又

所以因为函数在区间上的图像是连续不断的一条曲线，所以存在使即成立.

【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等，考查运算能力，考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出取最小值对一切x∈R，f(x) 1恒成立转化为从而得出求a的取值集合；第二问在假设存在的情况下进行推理，然后把问题归结为一个方程是否存在解的问题，通过构造函数，研究这个函数的性质进行分析判断.

已知函数f(x)＝alnx＋bx,且f(1)＝ －1，f′(1)＝0，

⑴求f(x)；

⑵求f(x)的最大值；

⑶若x＞0,y＞0,证明：lnx＋lny≤.

本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题，同时考查考生用函数放缩的方法证明不等式的能力．

（12分）先阅读下列框图，再解答有关问题：

（Ⅰ）当输入的分别为1，2，3时，各是多少？

（Ⅱ）当输入已知量时，

①输出的结果是什么？试证明之；

②输出S的结果是什么？写出求S的过程

（本小题满分10分）选修4－5：不等式选修

在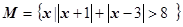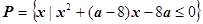，的前提下，求a的一个值，是它成为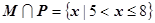的一个充分但不必要条件。

    2005年7月28日,BP位于美国得克萨斯市的炼油厂晚间发生爆炸,同样在7月28日,BP在其大本营英国北海的深水油田也发生了严重火灾.受其影响,全球油价7月29日再度突破60美元大关.随后沙特国王死亡引起对沙特政局的担忧,接下来一连串的飓风袭来,最后是飓风“卡特里娜”一举使油价突破70美元的大关,创下70.85美元/桶的历史记录.

    国际能源署IEA预计,到2005年底，飓风导致美国损失的原油以及天然气液化产量约1.4亿桶,成品油产量损失1.63亿桶.

    进入2006年,先是俄罗斯与乌克兰的石油管道问题,随后是基地组织将要袭击美国的威胁、尼日利亚的恐怖袭击以及伊朗的核问题不断出现，在美国气温高于往年平均气温导致需求不太旺盛的情况下,不到一个月的时间就将油价推高12美元/桶.可见突发事件对油价影响的巨大.

    在2005年原油的第二轮上涨中,基金持有的净多单数量远低于第一轮时的净多单,但是原油上涨的幅度远大于第一轮上涨的幅度,2005年9月以后基金绝大部分时间持有净空单,但是原油价格仍在高位,就是因为不断出现的突发消息助推油价.政治因素与突发事件导致的对原油供应不足的担忧,在原油上涨中可能起到20%—25%的作用.

(1)怎样理解“可见突发事件对油价影响的巨大”这句话的含义,如果是你,你将怎样得出这样的结论?

(2)为了尽量避免经济损失,我们应该怎样对经济进行统计分析?