(2)若M:m＝2.5.试求m运动到C点时的速度v,(3)简要描述m从A运动到B的过程中.M的速度变化情况.有一位同学在解第(1)小是顺时的思路是这样的:m在B点速度为零.所以所受合外力为零.列出方程——青夏教育精英家教网—

(2)若M:m＝2.5.试求m运动到C点时的速度v,(3)简要描述m从A运动到B的过程中.M的速度变化情况.有一位同学在解第(1)小是顺时的思路是这样的:m在B点速度为零.所以所受合外力为零.列出方程从而解出M:m.你认为该同学的解法正确吗?若认为正确.按该同学的思路列出第(1)小问的方程.不用算出.并完成第小问.若认为有错误.请说明理由.给出第(1)小问正确的解法.列出方程.不用算出.并完成第小问. 【查看更多】

如图所示，质量m＝50kg的运动员（可视为质点），在河岸上A点紧握一根长L＝5.0m的不可伸长的轻绳，轻绳另一端系在距离水面高H＝10.0m的O点，此时轻绳与竖直方向的夹角为θ＝37°，C点是位于O点正下方水面上的一点，距离C点x＝4.8m处的D点有一只救生圈，O、A、C、D各点均在同一竖直面内。若运动员抓紧绳端点，从台阶上A点沿垂直于轻绳斜向下以一定初速度v₀跃出，当摆到O点正下方的B点时松开手，最终恰能落在救生圈内。（sin37°=0.6，cos37°=0.8，g=10m/s²）求：
（1）运动员经过B点时速度的大小v₀；
（2）运动员从台阶上A点跃出时的动能E_k；
（3）若初速度v₀不一定，且使运动员最终仍能落在救生圈内，则救生圈离C点距离x将随运动员离开A点时初速度v₀的变化而变化。试在下面坐标系中粗略作出x－v₀的图像，并标出图线与x轴的交点。

查看答案和解析>>

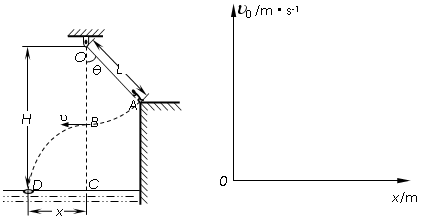
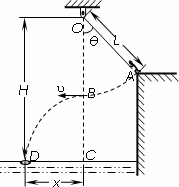
如图所示，质量m＝50 kg的运动员(可视为质点)，在河岸上A点紧握一根长L＝5.0 m的不可伸长的轻绳，轻绳另一端系在距离水面高H＝10.0 m的O点，此时轻绳与竖直方向的夹角为＝37°，C点是位于O点正下方水面上的一点，距离C点x＝4.8 m处的D点有一只救生圈，O、A、C、D各点均在同一竖直面内．若运动员抓紧绳端点，从台阶上A点沿垂直于轻绳斜向下以一定初速度v₀跃出，当摆到O点正下方的B点时松开手，最终恰能落在救生圈内．(sin37°＝0.6，cos37°＝0.8，g＝10 m/s²)求：

(1)运动员经过B点时速度的大小v_B；

(2)运动员从台阶上A点跃出时的动能E_k；

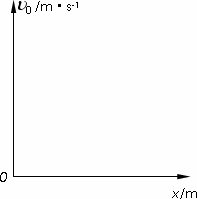
(3)若初速度v₀不一定，且使运动员最终仍能落在救生圈内，则救生圈离C点距离x将随运动员离开A点时初速度v₀的变化而变化．试在下面坐标系中粗略作出x－v₀的图像，并标出图线与x轴的交点．

查看答案和解析>>

如图10所示，一根直杆由粗细相同的两段构成，其中AB段为长x₁＝5 m的粗糙杆，BC段为长x₂＝1 m的光滑杆。将杆与水平面成53°角固定在一块弹性挡板上，在杆上套一质量m＝0.5 kg、孔径略大于杆直径的圆环。开始时，圆环静止在杆底端A。现用沿杆向上的恒力F拉圆环，当圆环运动到B点时撤去F，圆环刚好能到达顶端C，然后再沿杆下滑。已知圆环与AB段的动摩擦因数μ＝0.1，g＝10 m/s²，sin 53°＝0.8，cos 53°＝0.6。试求：

(1)拉力F的大小；

(2)拉力F作用的时间；

(3)若不计圆环与挡板碰撞时的机械能损失，从圆环开始运动到最终静止的过程中在粗糙杆上所通过的总路程。

图10

查看答案和解析>>

如图所示，是某公园设计的一种惊险刺激的娱乐设施，轨道除AB部分粗糙(μ＝0.125)外，其余均光滑，AB斜面与水平面夹角为37°．一挑战者质量为m＝60 kg，沿斜面轨道滑下，然后滑入第一个圆形轨道(轨道半径R＝2 m)，不计过B点时的能量损失，根据设计要求，在最低点与最高点各放一个压力传感器，测试挑战者对轨道的压力，并通过计算机显示出来．挑战者到达C处时刚好对轨道无压力，又经过水平轨道滑入第二个圆形轨道(轨道半径r＝1.6 m)，然后从平台上飞入水池内，水面离轨道的距离为h＝5 m．g取10 m/s²，人在运动全过程中可视为质点．求：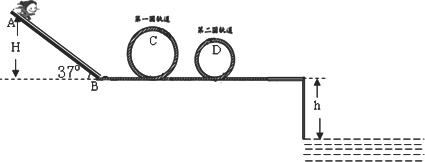

(1)在第二个圆形轨道的最高点D处挑战者对轨道的压力大小

(2)挑战者若能完成上述过程，则他应从离水平轨道多高的地方开始下滑

(3)挑战者入水时的速度大小是多少？方向如何？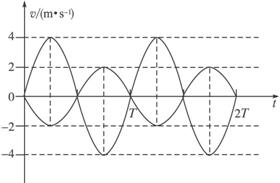

查看答案和解析>>

如图，光滑水平面上固定着一对竖直放置的平行金属板G和H。在金属板G右壁固定一个可视为质点的小球C，其质量为 M_c＝0.01 kg、带电荷量为q＝＋1×10^-5 C。G、H两板间距离为d＝10 cm，板H下方开有能让小球C自由通过的小洞。质量分别为M_a＝0.01 kg和M_b＝0.02 kg的不带电绝缘小球A、B用一轻质弹簧连接，并用细线拴连使弹簧处于压缩状态，静放在H板右侧的光滑水平面上，如图a所示。现将细线烧断，小球A、B在弹簧作用下做来回往复运动（A球不会进入G、H两板间）。以向右为速度的正方向，从细线断开后的某时刻开始计时，得到A球的速度—时间图象如图(b)所示。

图（a）

图（b）

（1）求在t=0、、时刻小球B的速度，并在图(b)中大致画出B球的速度—时间图象；

（2）若G、H板间是电场强度为E=8×10⁴ V/m的匀强电场，在某时刻将小球C释放，则小球C离开电场时的速度为多大？若小球C以离开电场时的速度向右匀速运动，它将遇到小球A，并与之结合在一起运动，试定量分析在各种可能的情况下弹簧的最大弹性势能（即最大弹性势能的范围）。

查看答案和解析>>

一、1、ACD 2、C 3、B 4、A 5、C 6、BC 7、BC 8、BD

二、实验题：（18分）将答案填在题目的空白处，或者要画图连线。

9、（6分）（BC）（4分），磁场总是要阻碍（2分）

10、（12分）(1)①“×1”欧姆挡(3分)

②9Ω(3分)

(2)①BDFGH(3分)

②如图所示(3分)

三、本大题共三小题共计54分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位

11、（16分）（1）m运动B点时速度为零，但不是平衡位置，所以受力不为零，（4分）（2）m运动C点时，M的速度为零，设M＝2m₀，则由机械能守恒得：5m₀gL cos60°sin60°＋2m₀gL（1－sin60°）＝´5m₀v²，v＝2.5m/s，（8分）（3）先由零逐渐增大后又逐渐减小到零，再逐渐增大后又逐渐减小到零。（4分）

12、（18分）(1)当小车上滑时，………………(1) (1分)