
题目列表(包括答案和解析)
在用单摆测重力加速度的实验中
(1)为了比较准确地测量出当地的重力加速度值,应选用下列所给器材中的哪些?将所选用的器材的字母填在题后的横线上.
(A)长1 m左右的细绳;
(B)长30 m左右的细绳;
(C)直径2 cm的铅球;
(D)直径2 cm的铁球;
(E)秒表;
(F)时钟;
(G)最小刻度是厘米的直尺;
(H)最小刻度是毫米的直尺.
所选择的器材是________.
(2)某同学测出不同摆长时对应的周期T,作出T2~L图线,如图所示,再利用图线上任两点A、B的坐标(x1,y1)、(x2,y2),可求得g=________.

(3)在本实验中,由于摆球形状不规则,无法准确测量摆长l,但摆线的长度![]() 可以准确测量.现使用同一摆球,多次改变摆线长度
可以准确测量.现使用同一摆球,多次改变摆线长度![]() 并测得每一次相应的摆动周期T,对于数据处理方法,下列说法中正确的是( )
并测得每一次相应的摆动周期T,对于数据处理方法,下列说法中正确的是( )
(A)![]() 与T2不是直线关系
与T2不是直线关系
(B)摆长l可以利用![]() -T2图线求出
-T2图线求出
(C)![]() 与T2是直线关系,在理论上,
与T2是直线关系,在理论上,![]() -T2直线的斜率与l-T2直线的相同
-T2直线的斜率与l-T2直线的相同
(D)![]() 与T2是直线关系,在理论上,
与T2是直线关系,在理论上,![]() -T2直线的斜率与l-T2直线的不同
-T2直线的斜率与l-T2直线的不同
(4)写出两条对提高实验结果准确程度有益的建议:
①________;
②________.
如图甲所示,真空中的电极K连续不断地发出电子(电子的初速度可忽略不计),经电压为Ul的电场加速,加速电压Ul随时间t变化的图象如图乙所示.每个电子通过加速电场的过程时间极短,可认为加速电压不变.电子被加速后由小孔S从穿出,设每秒K向加速电场发射的电子数目恒定.出加速电场后,电子沿两个彼此靠近且正对的水平金属板A、B间中轴线射入偏转电场,A、B两板长均为L=0.20 m,两板之间距离d=0.40 m,A板的电势比B板的电势高.A,B板右側边缘到竖直放置的荧光屏P(面积足够大)之间的距离b=0.20 m.荧光屏的中心点O与A、B板的中心轴线在同一水平直线上.不计电子之间的相互作用力及其所受的重力,求:
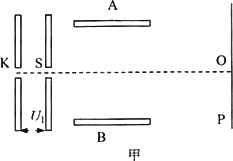
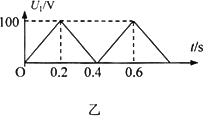
(1)要使电子都打不到荧光屏上,则A,B两板间所加电压U2应满足什么条件;
(2)当A、B板间所加电U2=200 V时,打到荧光屏上的电子距离中心点O在多大的范围内;
(3)在A、B间加适当的电压,在较长时间内可以使从加速电场中出来的电子90%都能打在荧光屏上,则此情况下所有能打到屏上的电子的动能的最小值为多少.
如图所示,A、B两条直线是A、B两地分别用竖直向上的力F拉质量分别为mA和mB的两个物体得出的加速度a与力F之间的关系图线,分析图线可知
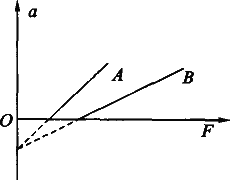
①比较两地的重力加速度,有gA>gB;
②比较两物体的质量,有mA<mB;
③比较两地的重力加速度,有gA=gB;
④比较两物体的质量,有mA>mB.
A.②③
B.①②
C.①④
D.③④
如图所示,A、B两条直线是在A、B两地分别用竖直向上的力F拉质量分别为![]() 和
和![]() 的两个物体得出的加速度a与力F之间的关系图线,分析图线可知:
的两个物体得出的加速度a与力F之间的关系图线,分析图线可知:
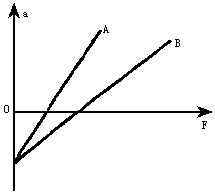
①比较两地的重力加速度,有![]() >
>![]() ;
;
②比较两物体的质量,有![]() <
<![]() ;
;
③比较两地的重力加速度,有![]() =
=![]() ;
;
④比较两物体的质量,有![]() >
>![]() .
.
其中正确的是
[ ]
第九部分 稳恒电流
第一讲 基本知识介绍
第八部分《稳恒电流》包括两大块:一是“恒定电流”,二是“物质的导电性”。前者是对于电路的外部计算,后者则是深入微观空间,去解释电流的成因和比较不同种类的物质导电的情形有什么区别。
应该说,第一块的知识和高考考纲对应得比较好,深化的部分是对复杂电路的计算(引入了一些新的处理手段)。第二块虽是全新的内容,但近几年的考试已经很少涉及,以至于很多奥赛培训资料都把它删掉了。鉴于在奥赛考纲中这部分内容还保留着,我们还是想粗略地介绍一下。
一、欧姆定律
1、电阻定律
a、电阻定律 R = ρ![]()
b、金属的电阻率 ρ = ρ0(1 + αt)
2、欧姆定律
a、外电路欧姆定律 U = IR ,顺着电流方向电势降落
b、含源电路欧姆定律

在如图8-1所示的含源电路中,从A点到B点,遵照原则:①遇电阻,顺电流方向电势降落(逆电流方向电势升高)②遇电源,正极到负极电势降落,负极到正极电势升高(与电流方向无关),可以得到以下关系
UA ? IR ? ε ? Ir = UB
这就是含源电路欧姆定律。
c、闭合电路欧姆定律
在图8-1中,若将A、B两点短接,则电流方向只可能向左,含源电路欧姆定律成为
UA + IR ? ε + Ir = UB = UA
即 ε = IR + Ir ,或 I = ![]()
这就是闭合电路欧姆定律。值得注意的的是:①对于复杂电路,“干路电流I”不能做绝对的理解(任何要考察的一条路均可视为干路);②电源的概念也是相对的,它可以是多个电源的串、并联,也可以是电源和电阻组成的系统;③外电阻R可以是多个电阻的串、并联或混联,但不能包含电源。
二、复杂电路的计算
1、戴维南定理:一个由独立源、线性电阻、线性受控源组成的二端网络,可以用一个电压源和电阻串联的二端网络来等效。(事实上,也可等效为“电流源和电阻并联的的二端网络”——这就成了诺顿定理。)
应用方法:其等效电路的电压源的电动势等于网络的开路电压,其串联电阻等于从端钮看进去该网络中所有独立源为零值时的等效电阻。
2、基尔霍夫(克希科夫)定律

a、基尔霍夫第一定律:在任一时刻流入电路中某一分节点的电流强度的总和,等于从该点流出的电流强度的总和。
例如,在图8-2中,针对节点P ,有
I2 + I3 = I1
基尔霍夫第一定律也被称为“节点电流定律”,它是电荷受恒定律在电路中的具体体现。
对于基尔霍夫第一定律的理解,近来已经拓展为:流入电路中某一“包容块”的电流强度的总和,等于从该“包容块”流出的电流强度的总和。
b、基尔霍夫第二定律:在电路中任取一闭合回路,并规定正的绕行方向,其中电动势的代数和,等于各部分电阻(在交流电路中为阻抗)与电流强度乘积的代数和。
例如,在图8-2中,针对闭合回路① ,有
ε3 ? ε2 = I3 ( r3 + R2 + r2 ) ? I2R2
基尔霍夫第二定律事实上是含源部分电路欧姆定律的变体(☆同学们可以列方程 UP = … = UP得到和上面完全相同的式子)。
3、Y?Δ变换

在难以看清串、并联关系的电路中,进行“Y型?Δ型”的相互转换常常是必要的。在图8-3所示的电路中
☆同学们可以证明Δ→ Y的结论…
Rc = ![]()
Rb = ![]()
Ra = ![]()
Y→Δ的变换稍稍复杂一些,但我们仍然可以得到
R1 = ![]()
R2 = ![]()
R3 = ![]()
三、电功和电功率
1、电源
使其他形式的能量转变为电能的装置。如发电机、电池等。发电机是将机械能转变为电能;干电池、蓄电池是将化学能转变为电能;光电池是将光能转变为电能;原子电池是将原子核放射能转变为电能;在电子设备中,有时也把变换电能形式的装置,如整流器等,作为电源看待。
电源电动势定义为电源的开路电压,内阻则定义为没有电动势时电路通过电源所遇到的电阻。据此不难推出相同电源串联、并联,甚至不同电源串联、并联的时的电动势和内阻的值。
例如,电动势、内阻分别为ε1 、r1和ε2 、r2的电源并联,构成的新电源的电动势ε和内阻r分别为(☆师生共同推导…)
ε = ![]()
r = ![]()
2、电功、电功率
电流通过电路时,电场力对电荷作的功叫做电功W。单位时间内电场力所作的功叫做电功率P 。
计算时,只有W = UIt和P = UI是完全没有条件的,对于不含源的纯电阻,电功和焦耳热重合,电功率则和热功率重合,有W = I2Rt = ![]() t和P = I2R =
t和P = I2R =![]() 。
。
对非纯电阻电路,电功和电热的关系依据能量守恒定律求解。
四、物质的导电性
在不同的物质中,电荷定向移动形成电流的规律并不是完全相同的。
1、金属中的电流
即通常所谓的不含源纯电阻中的电流,规律遵从“外电路欧姆定律”。
2、液体导电
能够导电的液体叫电解液(不包括液态金属)。电解液中离解出的正负离子导电是液体导电的特点(如:硫酸铜分子在通常情况下是电中性的,但它在溶液里受水分子的作用就会离解成铜离子Cu2+和硫酸根离子S![]() ,它们在电场力的作用下定向移动形成电流)。
,它们在电场力的作用下定向移动形成电流)。
在电解液中加电场时,在两个电极上(或电极旁)同时产生化学反应的过程叫作“电解”。电解的结果是在两个极板上(或电极旁)生成新的物质。
液体导电遵从法拉第电解定律——
法拉第电解第一定律:电解时在电极上析出或溶解的物质的质量和电流强度、跟通电时间成正比。表达式:m = kIt = KQ (式中Q为析出质量为m的物质所需要的电量;K为电化当量,电化当量的数值随着被析出的物质种类而不同,某种物质的电化当量在数值上等于通过1C电量时析出的该种物质的质量,其单位为kg/C。)
法拉第电解第二定律:物质的电化当量K和它的化学当量成正比。某种物质的化学当量是该物质的摩尔质量M(克原子量)和它的化合价n的比值,即 K = ![]() ,而F为法拉第常数,对任何物质都相同,F = 9.65×104C/mol 。
,而F为法拉第常数,对任何物质都相同,F = 9.65×104C/mol 。
将两个定律联立可得:m = ![]() Q 。
Q 。
3、气体导电
气体导电是很不容易的,它的前提是气体中必须出现可以定向移动的离子或电子。按照“载流子”出现方式的不同,可以把气体放电分为两大类——
a、被激放电
在地面放射性元素的辐照以及紫外线和宇宙射线等的作用下,会有少量气体分子或原子被电离,或在有些灯管内,通电的灯丝也会发射电子,这些“载流子”均会在电场力作用下产生定向移动形成电流。这种情况下的电流一般比较微弱,且遵从欧姆定律。典型的被激放电情形有
b、自激放电
但是,当电场足够强,电子动能足够大,它们和中性气体相碰撞时,可以使中性分子电离,即所谓碰撞电离。同时,在正离子向阴极运动时,由于以很大的速度撞到阴极上,还可能从阴极表面上打出电子来,这种现象称为二次电子发射。碰撞电离和二次电子发射使气体中在很短的时间内出现了大量的电子和正离子,电流亦迅速增大。这种现象被称为自激放电。自激放电不遵从欧姆定律。
常见的自激放电有四大类:辉光放电、弧光放电、火花放电、电晕放电。
4、超导现象
据金属电阻率和温度的关系,电阻率会随着温度的降低和降低。当电阻率降为零时,称为超导现象。电阻率为零时对应的温度称为临界温度。超导现象首先是荷兰物理学家昂尼斯发现的。
超导的应用前景是显而易见且相当广阔的。但由于一般金属的临界温度一般都非常低,故产业化的价值不大,为了解决这个矛盾,科学家们致力于寻找或合成临界温度比较切合实际的材料就成了当今前沿科技的一个热门领域。当前人们的研究主要是集中在合成材料方面,临界温度已经超过100K,当然,这个温度距产业化的期望值还很远。
5、半导体
半导体的电阻率界于导体和绝缘体之间,且ρ
1.C由电荷数守恒和质量数守恒可知A、B错,由于镍63放出电子,故带正电,电势比铜片电势高,C正确,电流方向从铜片到镍,D错
2.C
3.A由.files/image117.gif) 可知,A正确
可知,A正确
4.B将分子粗略地看成一个小立体,则.files/image119.gif) 个
个
5.D照射到a、b、c上三种光的频率关系,为.files/image121.gif) ,由光电效应的规律可知板b有电子射出,板c一定有光电子放出,正确答案为D
,由光电效应的规律可知板b有电子射出,板c一定有光电子放出,正确答案为D
6.A航天飞机的运行周期
.files/image123.gif)
设经过时间t航天飞机又通过建筑物上方,则
.files/image125.gif) ,所以
,所以.files/image127.gif)
7.A沿着电场线的方向电势降低,.files/image129.gif) ,B错;E、F两点在同一等势面上
,B错;E、F两点在同一等势面上.files/image131.gif) ,且
,且.files/image133.gif) ,A正确
,A正确
由等量异种电荷的等势面特点可知..files/image135.gif) ,C错,
,C错,.files/image137.gif) D错
D错
8.C.files/image139.gif) ①F=kA②
①F=kA②
由①②可知,C正确.
9.C先根据题意画出电子所走的.files/image141.jpg) 弧,因为弧上任意一点的速度方向必然与该点所在的半径垂直,故可以过A点做与
弧,因为弧上任意一点的速度方向必然与该点所在的半径垂直,故可以过A点做与.files/image055.gif) 方向(即AB方向)垂直的直线,此即为带电粒子做匀速圆周运动的半径方向.同理过C点作垂直于BC的直线,也为该点的半径方向,两半径相交点即为带电粒子做匀速圆周运动的圆心.如答图1所示.由图示情况可以看出
方向(即AB方向)垂直的直线,此即为带电粒子做匀速圆周运动的半径方向.同理过C点作垂直于BC的直线,也为该点的半径方向,两半径相交点即为带电粒子做匀速圆周运动的圆心.如答图1所示.由图示情况可以看出
.files/image144.jpg)
答图1
当.files/image146.gif) 时电子刚好不能从BC边射出.
时电子刚好不能从BC边射出.
要使电子可以从BC边射出,必满足r>.files/image148.gif) ,而r=
,而r=.files/image150.gif) ,
,
∴B<.files/image152.gif) 时,电子可以从BC边射出
时,电子可以从BC边射出
10.D11.(1)大于(2)轨道末端出口水平(3)P、.files/image073.gif) 、
、.files/image075.gif) 为落地的平均位置,F一步中的
为落地的平均位置,F一步中的.files/image156.gif) 应为
应为.files/image156.gif) -2r,
-2r,
12.(1)1.000
(2)①略
②A.将滑动变阻器调至输出电压为零的位置,再合上.files/image158.gif) .
.
B.将.files/image091.gif) 扳向2,调滑动变阻器使电流表指针在某一电流刻度,并记下该位置.
扳向2,调滑动变阻器使电流表指针在某一电流刻度,并记下该位置.
C.使.files/image089.gif) 阻值最大后,将
阻值最大后,将.files/image091.gif) 扳向1,调电阻箱,使电流表指针回到所记的位置,记下电阻箱阻值
扳向1,调电阻箱,使电流表指针回到所记的位置,记下电阻箱阻值.files/image089.gif) .
.
D.被测电阻.files/image087.gif) =
=.files/image089.gif) .
.
13.侦察卫星环绕地球一周,通过有日照的赤道一次,在卫星一个周期时间(设为.files/image164.gif) )地球自转的角度为q ,只要q 角所对应的赤道弧长能被拍摄下来,则一天时间内,地面上赤道处全部在有日照条件下就能被拍摄下来.设侦察卫量的周期为
)地球自转的角度为q ,只要q 角所对应的赤道弧长能被拍摄下来,则一天时间内,地面上赤道处全部在有日照条件下就能被拍摄下来.设侦察卫量的周期为.files/image164.gif) ,地球对卫星的万有引力为卫星做圆周运动的向心力,卫星的轨道半径r=R+h,根据牛顿第二定律,则
,地球对卫星的万有引力为卫星做圆周运动的向心力,卫星的轨道半径r=R+h,根据牛顿第二定律,则.files/image166.gif)
在地球表面的物体重力近似等于地球的万有引力,即mg=.files/image168.gif)
解得侦察卫星的周期为.files/image170.gif)
已知地球自转周期为T,则卫星绕行一周,地球自转的角度为q =2p?.files/image172.gif)
摄像机应拍摄赤道圆周的弧长为q 角所对应的圆周弧长应为
.files/image174.gif)
14.当开关S在位置1时,粒子在电容器中做类平抛运动,即水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,有
l=vt,.files/image176.gif)
得.files/image178.gif)
则带电粒子的初速度
.files/image180.gif) (m/s)
(m/s)
当S接到2位置时,电容器内形成按余弦规律变化的振荡电场,周期为
.files/image182.gif) .
.
接到位置2时,电容器内电场仍竖直向上,设粒子在第一个.files/image184.gif) 内加速向下运动,在第二个
内加速向下运动,在第二个.files/image184.gif) 内减速向下运动,在半个周期结束时,粒子的速度为零,平均加速度
内减速向下运动,在半个周期结束时,粒子的速度为零,平均加速度.files/image186.gif) <a,运动时间
<a,运动时间.files/image188.gif) <t,故粒子半个周期内竖直方向位移
<t,故粒子半个周期内竖直方向位移.files/image190.gif) ,粒子不会打到下极板上.
,粒子不会打到下极板上.
在第三个.files/image184.gif) 内,粒子加速向上运动,在第四个
内,粒子加速向上运动,在第四个.files/image184.gif) 内减速向上运动,在后半个周期结束时,粒子的速度为零.从对称性角度考虑,经过一个周期,粒子又回到两板中央,竖直方向速度为零.
内减速向上运动,在后半个周期结束时,粒子的速度为零.从对称性角度考虑,经过一个周期,粒子又回到两板中央,竖直方向速度为零.
不论电容器内电场如何作用周期性的变化,粒子在水平方向不受电场力的作用,水平速度不变,所以粒子在电场中运动的时间仍为2×.files/image192.gif) s,在这一时间内,电场做周期性变化的次数
s,在这一时间内,电场做周期性变化的次数
.files/image194.gif) .
.
所以当粒子离开电容器时,竖直速度为零,水平速度不变,仍为v=1.0×.files/image196.gif) m/s,从两板中央飞出.
m/s,从两板中央飞出.
所以粒子能飞出电容器,从两板中央水平飞出,v=1.00×.files/image196.gif) m/s.
m/s.
15.(1)滑块速度向右,根据匀速运动条件
.files/image198.gif) ①
①
可知E的方向必水平向右.
由返回速度向左且作匀速运动可知
.files/image200.gif) =mg ②
=mg ②
而题中有:.files/image202.gif) ③
③
②③联立得知.files/image204.gif) ,即
,即.files/image206.gif) =2mg,代入①式
=2mg,代入①式
所以E=m (mg+2mg)/q=3m mg/q
(2)设往返总时间为T有:
.files/image208.gif)
即:.files/image210.gif) ,代入②式可得
,代入②式可得.files/image212.gif)
(3)返回时不受摩擦力,所以全过程摩擦力做功
W=-fL=-m
(mg+.files/image206.gif) )L=-3m mgL
)L=-3m mgL
16.用答图2示平面内的光线进行分析,并只讨论从右侧观察的情形,如图所示,由亮点发出的任一光线CP线经过两次折射而从液面射出.由折射定律,按图上标记的各相关角度.有sina =nsinb ①
sing =(1/n)sind ②
其中d ≤p /2g =(p /2)-(b +j ) ③
.files/image214.jpg)
答图2
注意到,若液体内光线入射到液面上时发生全反射,就没有从液面射出的折射光线.全反射临界角.files/image216.gif) 满足条件sin
满足条件sin.files/image216.gif) =1/n
=1/n
可知光线CP经折射后能从液面射出从而可被观察到的条件为g <.files/image216.gif) ④
④
或sing <1/n⑤
现在计算sing .利用③式可得
sing =cos(b +j )=cosb cosj -sinb sinj
由①式可得cosb =.files/image218.gif)
因此,nsing =cosj .files/image220.gif) -nsinb sinj 又由①式nsing=cosj
-nsinb sinj 又由①式nsing=cosj .files/image220.gif) -sina sinj ⑥
-sina sinj ⑥
由图及①、②式,或由⑥式均可看出a 越大则g 越小,因此,如果与a 值最大的光线相应的g 设为.files/image222.gif) ,若
,若.files/image222.gif) >
>.files/image216.gif) ,则任何光线都不能射出液面.反之,只要
,则任何光线都不能射出液面.反之,只要.files/image222.gif) <
<.files/image216.gif) ,这部分光线就能射出液面,从液面上方可以观察到亮点.由此极端情况即可求出本题要求的条件.
,这部分光线就能射出液面,从液面上方可以观察到亮点.由此极端情况即可求出本题要求的条件.
自C点发出的a 值最大的光线是极靠近CD的光线,它被DB面折射后进入液体,由⑥式可知与之相应的.files/image222.gif)
a =(p /2)-j
nsin.files/image222.gif) =cosj
=cosj .files/image224.gif) -cosj sinj
-cosj sinj
能观察到亮点的条件为nsin.files/image222.gif) <1
<1
即cosj.files/image224.gif) -cosj sinj <1
-cosj sinj <1
上式可写成cosj.files/image224.gif) <1+cosj sinj
<1+cosj sinj
取平方.files/image228.gif)
化简.files/image230.gif)
故.files/image232.gif)
开方并化简可得.files/image234.gif)
这就是在液面上方从侧面适当的方向能看到亮点时n与j 之间应满足的条件.
17.(1)激光器的功率为.files/image107.gif) =NE①
=NE①
已知激光对物体表面的压力为F=2N?p②
由光压的定义.files/image237.gif) ③
③
联立以上各式得.files/image239.gif) ④
④
(2)太阳光对薄膜产生的光压
.files/image241.gif) ⑤
⑤
探测器受到的总光压力
F=I?S⑥
以探测器为研究对象,根据牛顿第二定律F=m?a ⑦
∴.files/image243.gif) ⑧
⑧
18.(1)由竖直上抛运动得炮弹被射出时的初速度.files/image245.gif) ①
①
(2)由动量守恒定律得:.files/image247.gif) ②
②
带电物体在洛仑兹力作用下的直线运动是匀速直线运动,假设电场强度方向竖直向上,根据受力有:.files/image249.gif) ③
③
.files/image251.gif) ④
④
联立②③④得:
两物体匀速运动的速度
∴.files/image253.gif)
.files/image255.gif)
所加电场为
.files/image257.gif) ⑦
⑦
因为E为正,所以场强方向竖直向上
(3)由动能定理得:爆炸对两物体做的功
.files/image259.gif) ⑧
⑧
.files/image261.gif) ⑨
⑨
(4)由平抛运动规律得落地时间:
.files/image263.gif) ⑩
⑩
两物体的水平位移
.files/image265.gif) =
=.files/image267.gif) =40×
=40×.files/image269.jpg)
.files/image271.gif) =
=.files/image273.gif) =50×
=50×
两物体落地点间的距离
Ds=.files/image265.gif) +
+.files/image271.gif) +L=360+20=
+L=360+20=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com