
题目列表(包括答案和解析)
如图10甲所示,ab、cd以为两根放置在同一水平面内且相互平行的金属轨道,相距L,右端连接一个阻值为R的定值电阻,轨道上放有一根导体棒MN,垂直两轨道且与两轨道接触良好,导体棒MN及轨道的电阻均可忽略不计。整个装置处于方向竖直向下的匀强磁场中,磁感应强度大小为B。导体棒MN在外办作用下以图中虚线所示范围的中心位置为平衡位置做简谐运动,振动周期为T,振幅为A,在t=0时刻恰好通过平衡位置,速度大小为v0,其简谐运动的速度V随时间t按余弦规律变化,如图10乙所示。则下列说法正确的是 ( )
|
B.导体棒MN中产生交流电的功率为![]()
C.通过导体棒MN的电流的有效值为![]()
D.在0![]() 等内通过导体棒MN的电荷量为
等内通过导体棒MN的电荷量为![]()
如图所示,在匀强磁场中,与磁感应强度B成30°角放置一矩形线圈,线圈长l1=10 cm、宽l2=8 cm,共100匝,线圈电阻r=1.0 Ω,与它相连的电路中,电阻R1=4.0 Ω,R2=5.0 Ω,电容C=50μF,磁感应强度变化如图乙所示,开关S在t0=0时闭合,在t2=1.5 s时又断开,求:
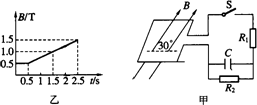
(1)t=1.0 s时,R2中电流的大小及方向;
(2)S断开后,通过R2的电量.
 如图乙所示,在匀强磁场中,与磁感应强度B成30°角放置一边长L=10cm的正方形线圈,共100匝,线圈电阻r=1Ω,与它相连的电路中,电阻R1=4Ω、R2=5Ω,电容C=10μF.磁感应强度变化如图甲所示,开关K在t0=0时闭合,在t2=1.5S时又断开.求:
如图乙所示,在匀强磁场中,与磁感应强度B成30°角放置一边长L=10cm的正方形线圈,共100匝,线圈电阻r=1Ω,与它相连的电路中,电阻R1=4Ω、R2=5Ω,电容C=10μF.磁感应强度变化如图甲所示,开关K在t0=0时闭合,在t2=1.5S时又断开.求: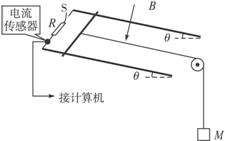
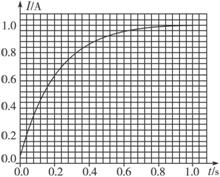
甲 乙
(1)匀强磁场的磁感应强度B的大小。
(2)0—0.2 s内,通过电阻R的电荷量。
(3)0—0.2 s内,电阻R上产生的焦耳热。
如图甲乙所示,在匀强磁场中,与磁感应强度B成![]() 角放置一边长L=10cm的正方形线圈,共100匝,线圈电阻r=1Ω,与它相连的电路中,电阻R1=4Ω、R2=5Ω,电容C=10μF.磁感应强度变化如图甲所示,开关K在t0=0时闭合,在t2=1.5S时又断开.求:
角放置一边长L=10cm的正方形线圈,共100匝,线圈电阻r=1Ω,与它相连的电路中,电阻R1=4Ω、R2=5Ω,电容C=10μF.磁感应强度变化如图甲所示,开关K在t0=0时闭合,在t2=1.5S时又断开.求:

①t1=1S时,R2中电流的大小及方向;
②K断开后,通过R2的电量.
1.C由电荷数守恒和质量数守恒可知A、B错,由于镍63放出电子,故带正电,电势比铜片电势高,C正确,电流方向从铜片到镍,D错
2.C
3.A由.files/image117.gif) 可知,A正确
可知,A正确
4.B将分子粗略地看成一个小立体,则.files/image119.gif) 个
个
5.D照射到a、b、c上三种光的频率关系,为.files/image121.gif) ,由光电效应的规律可知板b有电子射出,板c一定有光电子放出,正确答案为D
,由光电效应的规律可知板b有电子射出,板c一定有光电子放出,正确答案为D
6.A航天飞机的运行周期
.files/image123.gif)
设经过时间t航天飞机又通过建筑物上方,则
.files/image125.gif) ,所以
,所以.files/image127.gif)
7.A沿着电场线的方向电势降低,.files/image129.gif) ,B错;E、F两点在同一等势面上
,B错;E、F两点在同一等势面上.files/image131.gif) ,且
,且.files/image133.gif) ,A正确
,A正确
由等量异种电荷的等势面特点可知..files/image135.gif) ,C错,
,C错,.files/image137.gif) D错
D错
8.C.files/image139.gif) ①F=kA②
①F=kA②
由①②可知,C正确.
9.C先根据题意画出电子所走的.files/image141.jpg) 弧,因为弧上任意一点的速度方向必然与该点所在的半径垂直,故可以过A点做与
弧,因为弧上任意一点的速度方向必然与该点所在的半径垂直,故可以过A点做与.files/image055.gif) 方向(即AB方向)垂直的直线,此即为带电粒子做匀速圆周运动的半径方向.同理过C点作垂直于BC的直线,也为该点的半径方向,两半径相交点即为带电粒子做匀速圆周运动的圆心.如答图1所示.由图示情况可以看出
方向(即AB方向)垂直的直线,此即为带电粒子做匀速圆周运动的半径方向.同理过C点作垂直于BC的直线,也为该点的半径方向,两半径相交点即为带电粒子做匀速圆周运动的圆心.如答图1所示.由图示情况可以看出
.files/image144.jpg)
答图1
当.files/image146.gif) 时电子刚好不能从BC边射出.
时电子刚好不能从BC边射出.
要使电子可以从BC边射出,必满足r>.files/image148.gif) ,而r=
,而r=.files/image150.gif) ,
,
∴B<.files/image152.gif) 时,电子可以从BC边射出
时,电子可以从BC边射出
10.D11.(1)大于(2)轨道末端出口水平(3)P、.files/image073.gif) 、
、.files/image075.gif) 为落地的平均位置,F一步中的
为落地的平均位置,F一步中的.files/image156.gif) 应为
应为.files/image156.gif) -2r,
-2r,
12.(1)1.000
(2)①略
②A.将滑动变阻器调至输出电压为零的位置,再合上.files/image158.gif) .
.
B.将.files/image091.gif) 扳向2,调滑动变阻器使电流表指针在某一电流刻度,并记下该位置.
扳向2,调滑动变阻器使电流表指针在某一电流刻度,并记下该位置.
C.使.files/image089.gif) 阻值最大后,将
阻值最大后,将.files/image091.gif) 扳向1,调电阻箱,使电流表指针回到所记的位置,记下电阻箱阻值
扳向1,调电阻箱,使电流表指针回到所记的位置,记下电阻箱阻值.files/image089.gif) .
.
D.被测电阻.files/image087.gif) =
=.files/image089.gif) .
.
13.侦察卫星环绕地球一周,通过有日照的赤道一次,在卫星一个周期时间(设为.files/image164.gif) )地球自转的角度为q ,只要q 角所对应的赤道弧长能被拍摄下来,则一天时间内,地面上赤道处全部在有日照条件下就能被拍摄下来.设侦察卫量的周期为
)地球自转的角度为q ,只要q 角所对应的赤道弧长能被拍摄下来,则一天时间内,地面上赤道处全部在有日照条件下就能被拍摄下来.设侦察卫量的周期为.files/image164.gif) ,地球对卫星的万有引力为卫星做圆周运动的向心力,卫星的轨道半径r=R+h,根据牛顿第二定律,则
,地球对卫星的万有引力为卫星做圆周运动的向心力,卫星的轨道半径r=R+h,根据牛顿第二定律,则.files/image166.gif)
在地球表面的物体重力近似等于地球的万有引力,即mg=.files/image168.gif)
解得侦察卫星的周期为.files/image170.gif)
已知地球自转周期为T,则卫星绕行一周,地球自转的角度为q =2p?.files/image172.gif)
摄像机应拍摄赤道圆周的弧长为q 角所对应的圆周弧长应为
.files/image174.gif)
14.当开关S在位置1时,粒子在电容器中做类平抛运动,即水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,有
l=vt,.files/image176.gif)
得.files/image178.gif)
则带电粒子的初速度
.files/image180.gif) (m/s)
(m/s)
当S接到2位置时,电容器内形成按余弦规律变化的振荡电场,周期为
.files/image182.gif) .
.
接到位置2时,电容器内电场仍竖直向上,设粒子在第一个.files/image184.gif) 内加速向下运动,在第二个
内加速向下运动,在第二个.files/image184.gif) 内减速向下运动,在半个周期结束时,粒子的速度为零,平均加速度
内减速向下运动,在半个周期结束时,粒子的速度为零,平均加速度.files/image186.gif) <a,运动时间
<a,运动时间.files/image188.gif) <t,故粒子半个周期内竖直方向位移
<t,故粒子半个周期内竖直方向位移.files/image190.gif) ,粒子不会打到下极板上.
,粒子不会打到下极板上.
在第三个.files/image184.gif) 内,粒子加速向上运动,在第四个
内,粒子加速向上运动,在第四个.files/image184.gif) 内减速向上运动,在后半个周期结束时,粒子的速度为零.从对称性角度考虑,经过一个周期,粒子又回到两板中央,竖直方向速度为零.
内减速向上运动,在后半个周期结束时,粒子的速度为零.从对称性角度考虑,经过一个周期,粒子又回到两板中央,竖直方向速度为零.
不论电容器内电场如何作用周期性的变化,粒子在水平方向不受电场力的作用,水平速度不变,所以粒子在电场中运动的时间仍为2×.files/image192.gif) s,在这一时间内,电场做周期性变化的次数
s,在这一时间内,电场做周期性变化的次数
.files/image194.gif) .
.
所以当粒子离开电容器时,竖直速度为零,水平速度不变,仍为v=1.0×.files/image196.gif) m/s,从两板中央飞出.
m/s,从两板中央飞出.
所以粒子能飞出电容器,从两板中央水平飞出,v=1.00×.files/image196.gif) m/s.
m/s.
15.(1)滑块速度向右,根据匀速运动条件
.files/image198.gif) ①
①
可知E的方向必水平向右.
由返回速度向左且作匀速运动可知
.files/image200.gif) =mg ②
=mg ②
而题中有:.files/image202.gif) ③
③
②③联立得知.files/image204.gif) ,即
,即.files/image206.gif) =2mg,代入①式
=2mg,代入①式
所以E=m (mg+2mg)/q=3m mg/q
(2)设往返总时间为T有:
.files/image208.gif)
即:.files/image210.gif) ,代入②式可得
,代入②式可得.files/image212.gif)
(3)返回时不受摩擦力,所以全过程摩擦力做功
W=-fL=-m
(mg+.files/image206.gif) )L=-3m mgL
)L=-3m mgL
16.用答图2示平面内的光线进行分析,并只讨论从右侧观察的情形,如图所示,由亮点发出的任一光线CP线经过两次折射而从液面射出.由折射定律,按图上标记的各相关角度.有sina =nsinb ①
sing =(1/n)sind ②
其中d ≤p /2g =(p /2)-(b +j ) ③
.files/image214.jpg)
答图2
注意到,若液体内光线入射到液面上时发生全反射,就没有从液面射出的折射光线.全反射临界角.files/image216.gif) 满足条件sin
满足条件sin.files/image216.gif) =1/n
=1/n
可知光线CP经折射后能从液面射出从而可被观察到的条件为g <.files/image216.gif) ④
④
或sing <1/n⑤
现在计算sing .利用③式可得
sing =cos(b +j )=cosb cosj -sinb sinj
由①式可得cosb =.files/image218.gif)
因此,nsing =cosj .files/image220.gif) -nsinb sinj 又由①式nsing=cosj
-nsinb sinj 又由①式nsing=cosj .files/image220.gif) -sina sinj ⑥
-sina sinj ⑥
由图及①、②式,或由⑥式均可看出a 越大则g 越小,因此,如果与a 值最大的光线相应的g 设为.files/image222.gif) ,若
,若.files/image222.gif) >
>.files/image216.gif) ,则任何光线都不能射出液面.反之,只要
,则任何光线都不能射出液面.反之,只要.files/image222.gif) <
<.files/image216.gif) ,这部分光线就能射出液面,从液面上方可以观察到亮点.由此极端情况即可求出本题要求的条件.
,这部分光线就能射出液面,从液面上方可以观察到亮点.由此极端情况即可求出本题要求的条件.
自C点发出的a 值最大的光线是极靠近CD的光线,它被DB面折射后进入液体,由⑥式可知与之相应的.files/image222.gif)
a =(p /2)-j
nsin.files/image222.gif) =cosj
=cosj .files/image224.gif) -cosj sinj
-cosj sinj
能观察到亮点的条件为nsin.files/image222.gif) <1
<1
即cosj.files/image224.gif) -cosj sinj <1
-cosj sinj <1
上式可写成cosj.files/image224.gif) <1+cosj sinj
<1+cosj sinj
取平方.files/image228.gif)
化简.files/image230.gif)
故.files/image232.gif)
开方并化简可得.files/image234.gif)
这就是在液面上方从侧面适当的方向能看到亮点时n与j 之间应满足的条件.
17.(1)激光器的功率为.files/image107.gif) =NE①
=NE①
已知激光对物体表面的压力为F=2N?p②
由光压的定义.files/image237.gif) ③
③
联立以上各式得.files/image239.gif) ④
④
(2)太阳光对薄膜产生的光压
.files/image241.gif) ⑤
⑤
探测器受到的总光压力
F=I?S⑥
以探测器为研究对象,根据牛顿第二定律F=m?a ⑦
∴.files/image243.gif) ⑧
⑧
18.(1)由竖直上抛运动得炮弹被射出时的初速度.files/image245.gif) ①
①
(2)由动量守恒定律得:.files/image247.gif) ②
②
带电物体在洛仑兹力作用下的直线运动是匀速直线运动,假设电场强度方向竖直向上,根据受力有:.files/image249.gif) ③
③
.files/image251.gif) ④
④
联立②③④得:
两物体匀速运动的速度
∴.files/image253.gif)
.files/image255.gif)
所加电场为
.files/image257.gif) ⑦
⑦
因为E为正,所以场强方向竖直向上
(3)由动能定理得:爆炸对两物体做的功
.files/image259.gif) ⑧
⑧
.files/image261.gif) ⑨
⑨
(4)由平抛运动规律得落地时间:
.files/image263.gif) ⑩
⑩
两物体的水平位移
.files/image265.gif) =
=.files/image267.gif) =40×
=40×.files/image269.jpg)
.files/image271.gif) =
=.files/image273.gif) =50×
=50×
两物体落地点间的距离
Ds=.files/image265.gif) +
+.files/image271.gif) +L=360+20=
+L=360+20=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com