如图给出的是物体的运动图象，纵坐标v表示速度，横坐标t表示时间，其中哪一个在现实生活中是不可能存在的（　　）

A．

B．

C．

D．

查看答案和解析>>

如图给出的是物体的运动图象，纵坐标v表示速度，横坐标t表示时间，其中哪一个在现实生活中是不可能存在的（ ）
A．
B．
C．
D．

查看答案和解析>>

查看答案和解析>>

（2009?宁波模拟）如图给出的是物体的运动图象，纵坐标v表示速度，横坐标t表示时间，其中哪一个在现实生活中是不可能存在的（　　）

A．

B．

C．

D．

查看答案和解析>>

（1）用图1示装置研究平抛物体的运动．实验时在地面铺上复写纸和白纸，使小球（视为质点）从斜槽上紧靠挡板处由静止滑下，小球落地后将在白纸上留下痕迹．通过测量斜糟末端到地面的高度h和小球的水平射程x，即可计算出小球平抛的初速度r₄．

以下关于该实验的说法中合理的是

BD

BD

．
A．实验所用的斜糟必须光滑B．实验所用的斜糟末端初切线必须水平
C．实验时还能要使用秒表测出小球落地的时间
D．为精确确定落点位置，应让小球从同一亮度多次下落，用尽可能小的圆将白纸上小球留下的痕迹圆在其内，其圆心就是小球的平均落点．
（2）某同学在做“利用单摆测重力加速度”的实验时，透过改变摆长l调出相应的周期T，得出一组对应的l与T的数，再以l为横坐标，T²为纵坐标将所得数据连成直线，若求得该直线的斜率为K，则重力加速度g=

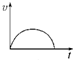
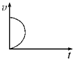
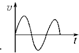
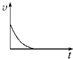
4m2

K

4m2

K

．若该同学在测摆长时漏测了小球半径，则用这种作图法求出的重力加速度和没有漏测小球半径相比

没有影响

没有影响

（选填“偏大”、“偏小”或“没有影响”）．
（3）某同学利用图2示电路测电池的电动势和内电阻，记录的6组数据如表格所示．

U（V）	I（A）
1.37	0.12
1.32	0.20
1.24	0.31
1.18	0.32
1.10	0.50
1.05	0.57

①为了使实验结果相对精确，请根据数据分布的特点，在给出的U-I坐标轴上标上合现的坐标值，并作出U-I图象3．
②根据图象3求出电池的电动势E=

1.44～1.48

1.44～1.48

V，电池的内电阻r=

0.65～0.75

0.65～0.75

Ω．

查看答案和解析>>

         （2）A₁      R₁

23 . （14 分）跳水是一项优美的水上运动，图甲是 2008 年北京奥运会跳水比赛中小将陈若琳和王鑫在跳台上腾空而起的英姿。如果陈若琳质量为 m ，身高为 L ，她站在离水面 H 高的跳台上，重心离跳台面的高度为 h_l ，竖直向上跃起后重心又升高了 h₂ 达到最高点，入水时身体竖直，当手触及水面时伸直双臂做一个翻掌压水花的动作，如图乙所示，这时陈若琳的重心离水面约为 h₃ ，她进入水中后重心最低可到达水面下 h₄ 处，整个过程中空气阻力可忽略不计，重力加速度为 g , 求：

（l）求陈若琳从离开跳台到手触及水面的过程中可用于完成一系列动作的时间；

（2）求陈若琳克服水的作用力所做的功。

解：（l）陈若琳跃起后可看作竖直向上的匀减速运动，重心上升的高度h₂,设起跳速度为v₀, 则  

上升过程时间  解得：        （2分）

陈若琳从最高处自由下落到手触及水面的过程中重心下落的高度

       （2分）

设下落过程时间为t₂    则  

解得：    （2分）

总时间为   （2分）

( 2 ）设从最高点到水面下最低点的过程中，重力做的功为W_G，克服水的作用力的功为W_Z    由动能定理可得  （2分）

     ( 4 分）

24 . ( 18 分）如图，阻值不计的光滑金属导轨MN和PQ 水平放置，其最右端间距 d 为 lm ，左端MP接有阻值 r 为 4Ω 的电阻，右端NQ与半径 R 为 2m 的光滑竖直半圆形绝缘导轨平滑连接；一根阻值不计的长为 L = l . 2m ，质量 m＝0.5kg 的金属杆 ab 放在导轨的 EF 处， EF 与MP平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场 B ,平面NQDC的右侧空间中无磁场。现杆 ab 以初速度V₀ = 12m / s 向右在水平轨道上做匀减速运动，进入半圆形导轨后恰能通过最高位置 CD 并恰又落到 EF 位置； ( g 取 10m / s2 ) 求： （l）杆 ab 刚进入半圆形导轨时，对导轨的压力；

（2）EF 到QN的距离；

（3）磁感应强度 B 的大小

解： ( 1 ）设杆ab刚进入半圆形导轨时速度为V₁到达最高位置，速度为V₂，由于恰能通过最高点，则：

   得：   （2分）

杆 ab 进入半圆形导轨后，由于轨道绝缘，无感应电流，则根据机械能守恒：

    得：   （2分）

设在最低点时半圆形轨道对杆 ab 的支持力为 N

   N＝30N  （2分）

( 2 )好 ab 离开半圆形导轨后做平抛运动，设经时间 t 落到水平导轨上

      （2分）

则杆 ab 与 NQ 的水平距离 S ＝4m 故 EF 与 NQ 的水平距离为4m  （2分）

（3）设杆 ab 做匀减速运动的加速度为 a

    得：a=-5.5m/s²      （2分）

对杆刚要到达 NQ 位置处进行分析

（2分）     （2分） 

25 . ( 22 分）如图，空间XOY 的第一象限存在垂直XOY 平面向里的匀强磁场，第四象限存在平行该平面的匀强电场（图中未画出） : OMN 是一绝缘弹性材料制成的等边三角形框架，边长 L 为 4m ，OM边上的 P 处开有一个小孔，OP距离为 lm 。现有一质量 m 为 l ×10^－18kg，电量 q 为 1 ×10^－15C带电微粒（重力不计）从 Y 轴上的C点以速度 V₀ = l00 m/s平行 x 轴射入，刚好可以垂直 x 轴从P点进入框架， CO 距离为 2m 。粒子进入框架后与框架发生若干次垂直的弹性碰撞，碰撞过程中粒子的电量和速度大小均保持不变，速度方向与碰前相反，最后粒子又从P点垂直 x 轴射出，求：

（l）所加电场强度的大小；

（2）所加磁场磁感应强度大小；

（3）求在碰撞次数最少的情况下，该微粒回到 C 点的时间间隔；