
题目列表(包括答案和解析)
一支车队有15辆车,某天依次出发执行运输任务,第一辆车于下午2时出发,第二辆车于下午2时10分出发,第三辆车于下午2时20分出发,依此类推。假设所有的司机都连续开车,并都在下午6时停下来休息。
(1)到下午6时最后一辆车行驶了多长时间?
(2)如果每辆车的行驶速度都是60 ,这个车队当天一共行驶了多少千米?
,这个车队当天一共行驶了多少千米?
【解析】第一问中,利用第一辆车出发时间为下午2时,每隔10分钟即 小时出发一辆
小时出发一辆
则第15辆车在 小时,最后一辆车出发时间为:
小时,最后一辆车出发时间为: 小时
小时
第15辆车行驶时间为: 小时(1时40分)
小时(1时40分)
第二问中,设每辆车行驶的时间为: ,由题意得到
,由题意得到
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
则行驶的总时间为:
则行驶的总里程为: 运用等差数列求和得到。
运用等差数列求和得到。
解:(1)第一辆车出发时间为下午2时,每隔10分钟即 小时出发一辆
小时出发一辆
则第15辆车在 小时,最后一辆车出发时间为:
小时,最后一辆车出发时间为: 小时
小时
第15辆车行驶时间为: 小时(1时40分)
……5分
小时(1时40分)
……5分
(2)设每辆车行驶的时间为: ,由题意得到
,由题意得到
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
则行驶的总时间为: ……10分
……10分
则行驶的总里程为:
已知数列 是公差不为零的等差数列,
是公差不为零的等差数列,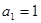 ,且
,且 、
、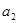 、
、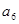 成等比数列。
成等比数列。
⑴求数列 的通项公式;
的通项公式;
⑵设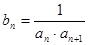 ,求数列
,求数列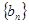 的前
的前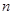 项和
项和 。
。
【解析】第一问中利用等差数列 的首项为
的首项为 ,公差为d,则依题意有:
,公差为d,则依题意有:
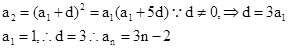
第二问中,利用第一问的结论得到数列的通项公式,
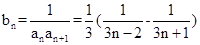 ,利用裂项求和的思想解决即可。
,利用裂项求和的思想解决即可。
已知函数
 ;
;
(1)若函数 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数 的取值范围。
的取值范围。
(2)若函数 ,若在[1,e]上至少存在一个x的值使
,若在[1,e]上至少存在一个x的值使 成立,求实数
成立,求实数 的取值范围。
的取值范围。
【解析】第一问中,利用导数 ,因为
,因为 在其定义域内的单调递增函数,所以
在其定义域内的单调递增函数,所以 内满足
内满足 恒成立,得到结论第二问中,在[1,e]上至少存在一个x的值使
恒成立,得到结论第二问中,在[1,e]上至少存在一个x的值使 成立,等价于不等式
成立,等价于不等式 在[1,e]上有解,转换为不等式有解来解答即可。
在[1,e]上有解,转换为不等式有解来解答即可。
解:(1) ,
,
因为 在其定义域内的单调递增函数,
在其定义域内的单调递增函数,
所以 内满足
内满足 恒成立,即
恒成立,即 恒成立,
恒成立,
亦即 ,
,
 即可 又
即可 又
当且仅当 ,即x=1时取等号,
,即x=1时取等号,
 在其定义域内为单调增函数的实数k的取值范围是
在其定义域内为单调增函数的实数k的取值范围是 .
.
(2)在[1,e]上至少存在一个x的值使 成立,等价于不等式
成立,等价于不等式 在[1,e]上有解,设
在[1,e]上有解,设

 上的增函数,
上的增函数, 依题意需
依题意需
 实数k的取值范围是
实数k的取值范围是
已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中 ,那么当
,那么当 时,
时, 又
又  所以函数
所以函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 ;(2)中令
;(2)中令 有
有 

对a分类讨论 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 当 时,
时, 又
又 
∴ 函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令 有
有 

①
当 即
即 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,

∴  在区间
在区间 上为增函数,则
上为增函数,则
依题意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(
 ,
, )
)
如图, ,
,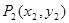 ,…,
,…, ,…是曲线
,…是曲线 上的点,
上的点, ,
, ,…,
,…, ,…是
,…是 轴正半轴上的点,且
轴正半轴上的点,且 ,
, ,…,
,…, ,…
均为斜边在
,…
均为斜边在 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点).
(1)写出 、
、 和
和 之间的等量关系,以及
之间的等量关系,以及 、
、 和
和 之间的等量关系;
之间的等量关系;
(2)求证: (
( );
);
(3)设 ,对所有
,对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.

【解析】第一问利用有 ,
, 得到
得到
第二问证明:①当 时,可求得
时,可求得 ,命题成立;②假设当
,命题成立;②假设当 时,命题成立,即有
时,命题成立,即有 则当
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得
第三问

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即

解:(1)依题意,有 ,
, ,………………4分
,………………4分
(2)证明:①当 时,可求得
时,可求得 ,命题成立;
……………2分
,命题成立;
……………2分
②假设当 时,命题成立,即有
时,命题成立,即有 ,……………………1分
,……………………1分
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得 .
.
即
解得 (
( 不合题意,舍去)
不合题意,舍去)
即当 时,命题成立. …………………………………………4分
时,命题成立. …………………………………………4分
综上所述,对所有 ,
, . ……………………………1分
. ……………………………1分
(3)

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即
 .……………2分
.……………2分
由题意,有
 .
所以,
.
所以,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com