
题目列表(包括答案和解析)
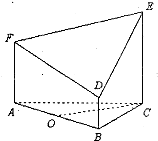 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.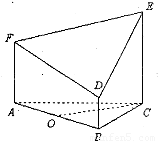
①底面是三角形,其余的各面是全等的等腰三角形的棱锥是正三棱锥;②底面是三角形,侧面和底面所在的平面所成的锐二面角相等的棱锥是正三棱锥;③一个棱锥是正棱锥的充分必要条件是底面多边形既有内切圆,又有外接圆,而且是同心圆;④一个四棱锥是正四棱锥的充分但不必要条件是各侧面是等边三角形.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
以下四个命题:
①如果两个平面垂直,则其中一个平面内的任意一条直线都垂直于另一个平面内无数条直线;②设m、n为两条不同的直线, 、
、 是两个不同的平面,若
是两个不同的平面,若 ,
, ,③“直线
,③“直线 ”的充分而不必要条件是“
”的充分而不必要条件是“ 垂直于
垂直于 在平面
在平面 内的射影”;④若点P到一个三角形三条边的距离相等,则点P在该三角形所在平面上的射影是该三家形的内心。其中正确的命题序号为 。
内的射影”;④若点P到一个三角形三条边的距离相等,则点P在该三角形所在平面上的射影是该三家形的内心。其中正确的命题序号为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com