
题目列表(包括答案和解析)
为了了解某市工人开展体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,计算这2个工厂中至少有1个来自A区的概率.
【解析】本试题主要考查了统计和概率的综合运用。
第一问工厂总数为18+27+18=63,样本容量与总体中的个体数比为7/63=1/9…3分
所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2。
第二问设A1,A2为在A区中的抽得的2个工厂,B1,B2,B3为在B区中抽得的3个工厂,
C1,C2为在C区中抽得的2个工厂。
这7个工厂中随机的抽取2个,全部的可能结果有1/2*7*6=32种。
随机的抽取的2个工厂至少有一个来自A区的结果有A1,A2),A1,B2),A1,B1),
A1,B3)A1,C2),A1,C1), …………9分
同理A2还能给合5种,一共有11种。
所以所求的概率为p=11/21
如图,边长为2的正方形ABCD,E是BC的中点,沿AE,DE将 折起,使得B与C重合于O.
折起,使得B与C重合于O.
(Ⅰ)设Q为AE的中点,证明:QD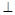 AO;
AO;
(Ⅱ)求二面角O—AE—D的余弦值.
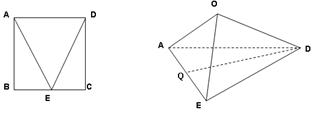
【解析】第一问中,利用线线垂直,得到线面垂直,然后利用性质定理得到线线垂直。取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
第二问中,作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=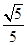 ,DN=
,DN= ,COS
,COS DNM=
DNM=
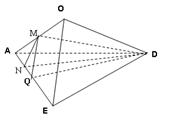
(1)取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
(2)作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=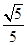 ,DN=
,DN= ,COS
,COS DNM=
DNM=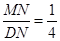
二面角O-AE-D的平面角的余弦值为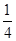
两个盒内分别盛着写有0,1,2,3,4,5六个数字的六张卡片,若从每盒中各取一张,求所取两数之和等于6的概率,现有甲、乙两人分别给出的一种解法:
甲的解法:因为两数之和可有0,1,2,…,10共11种不同的结果,所以所求概率为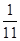 .
.
乙的解法:从每盒中各取一张卡片,共有36种取法,其中和为6的情况有5种:(1,5)、(5,1)、(2,4)、(4,2)、(3,3)因此所求概率为 .
.
试问哪一种解法正确?为什么?
如图,在四棱锥 中,底面 是边长为1的菱形, , 底面 , , 为 的中点.
(Ⅰ)求异面直线AB与MD所成角的大小;
(Ⅱ)求平面 与平面 所成的二面角的余弦值.
| 3 | 16 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com