
题目列表(包括答案和解析)
(12分)一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为![]() ,出现“×”的概率为
,出现“×”的概率为![]() .若第
.若第![]() 次出现“○”,则a
次出现“○”,则a![]() =1;出现“×”,则a
=1;出现“×”,则a![]() =
=![]() .令S
.令S![]() =a
=a![]() +a
+a![]() +…+a
+…+a![]()
![]() .
.
(1)当![]() 时,求S
时,求S![]()
![]() 2的概率;
2的概率;
(12分)甲、乙二人各有6张扑克牌,每人都是3张红心,2张草花,1张方片。每次两人从自己的6张牌中任意抽取一张进行比较,规定:两人花色相同时甲胜,花色不同时乙胜。
(Ⅰ)此规定是否公平?为什么?
(Ⅱ)若又规定:当甲取红心、草花、方片而获胜所得的分数分别为3、2、1,否则得0分,求甲得分的期望.
(12分) 已知集合A={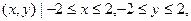 },
},
集合B={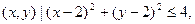 }.
}.
(1)在集合A中任取一个元素P,求P∈B的概率;
(2)若集合A,B中元素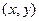 的
的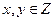 ,则在集合A中任取一个元素P,求P∈B的概率.
,则在集合A中任取一个元素P,求P∈B的概率.
12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
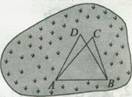
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
(12分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;(6分)
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X). (6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com