
题目列表(包括答案和解析)
(09年莱阳一中期末理)(12分)四棱锥![]() 中,
中,
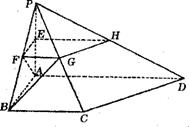
![]() ,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,
,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,![]() ,
,![]() 。
。
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为![]() ,求cos
,求cos![]() .
.
(09年莱阳一中期末文)(14分)
已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率为
的焦点,离心率为![]() 。
。
(1) 求椭圆![]() 的标准方程;
的标准方程;
(2) 过椭圆![]() 的右焦点作直线
的右焦点作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() 的值。
的值。
(09年莱阳一中期末文)(12分)
我们用部分自然数构造如下的数表:用![]()
![]() 表示第
表示第![]() 行第
行第![]() 个数为整数
个数为整数![]() ,使
,使![]() ;每行中的其余各数分别等于其‘肩膀”上的两个数之和(第一、二行除外,如图),设第
;每行中的其余各数分别等于其‘肩膀”上的两个数之和(第一、二行除外,如图),设第![]() (
(![]() 为正整数)行中各数之和为
为正整数)行中各数之和为![]() 。
。

(1) 试写出![]() 并推测
并推测![]() 和
和![]() 的关系(无需证明);
的关系(无需证明);
(2) 证明数列![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式
的通项公式![]() ;
;
(3) 数列![]() 中是否存在不同的三项
中是否存在不同的三项![]() 恰好成等差数列?若存在求出
恰好成等差数列?若存在求出![]() 的关系;若不存在,请说明理由。
的关系;若不存在,请说明理由。
(09年莱阳一中期末)(12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() 。
。
(1)求函数![]() 的最小正周期和在
的最小正周期和在![]() 上的单调递增区间;
上的单调递增区间;
(2)当![]() 时,
时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(09年莱阳一中期末文)(12分)
如图,已知三棱锥![]() 中,
中,![]()
![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,且△
中点,且△![]() 为正三角形。
为正三角形。
(1) 求证:![]() ∥平面
∥平面![]() ;
;
(2) 求证:平面![]() 平面
平面![]() ;
;
(3) 若![]()
![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积。
的体积。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com