
题目列表(包括答案和解析)
 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):如图,ABCD是边长为2的正方形纸片,沿某动直线![]() 为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为
为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为![]() ;折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB。若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
;折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB。若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
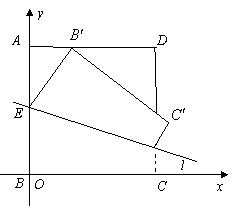 (Ⅰ).求点M的轨迹方程;
(Ⅰ).求点M的轨迹方程;
(Ⅱ).若曲线S是由点M的轨迹及其关于边AB对称的曲线组成的,等腰梯形![]() 的三边
的三边![]() 分别与曲线S切于点
分别与曲线S切于点![]() .求梯形
.求梯形![]() 面积的最小值.
面积的最小值.

(本小题满分12分)已知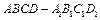 是边长为1的正方体,求:
是边长为1的正方体,求:
⑴直线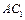 与平面
与平面 所成角的正切值;
所成角的正切值;
⑵二面角 的大小;
的大小;
⑶求点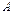 到平面
到平面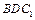 的距离。
的距离。
已知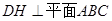 垂足为
垂足为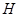 ,
,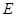 是
是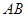 的中点且
的中点且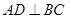 ,
,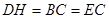 ,
,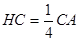 .
.
(1) 求证:平面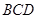
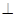 平面
平面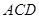 ;
;
(2) 求直线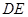 与平面
与平面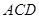 所成角的正切值.
所成角的正切值.

一、选择题:本大题共8题,每小题5分,共40分。
题号
1
2
3
4
5
6
7
8
答案
D
B
D
B
C
A
B
B
二、填空题:本大题共7小题,每小题5分,共30分。
9.55 10.-3 11..files/image181.gif) 12.
12..files/image183.gif) 13.1 14.2 15.
13.1 14.2 15..files/image185.gif)
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题满分12分)
已知向量.files/image187.gif) ,
,.files/image126.gif) ,
,.files/image189.gif) ,设
,设.files/image191.gif) .
.
(I)求函数.files/image132.gif) 的最小正周期。(II)
的最小正周期。(II).files/image134.gif) ,求
,求.files/image193.gif) 的值域。
的值域。
解:(I)因为.files/image195.gif)
.files/image197.gif) ………………………………………………………4分
………………………………………………………4分
所以函数.files/image132.gif) 的最小正周期
的最小正周期.files/image199.gif) .……………………………………6分
.……………………………………6分
(II)因为.files/image134.gif) ,
,
.files/image201.gif) ………………………………………………………………………8分
………………………………………………………………………8分
所以.files/image203.gif) ……………………………………………………………10分
……………………………………………………………10分
所以.files/image205.gif) 。 ……………………………………………………………… 12分
。 ……………………………………………………………… 12分
17.(本小题满分12分)
(1).files/image207.gif) ; ………………………………………………………4分
; ………………………………………………………4分
(2).files/image209.gif) ; …………………………………………………………… 8分
; …………………………………………………………… 8分
(3)表面积S=48. ……………………………………………………………… 12分
18.(本小题满分14分)
解答(1)x=1+1+1=3 或者x=-
(2)
i
I=3
I=5
P
(0.53)+ (0.53)=0.25
1-0.25=0.75
Ei=3×0.25+5×0.75=4.5---------------(8分)
(3)
ξ
ξ=1
ξ=3
P
18×0.55=.files/image211.gif)
6×0.55+2×0.53=.files/image213.gif)
Eξ=1×.files/image211.gif) +3×
+3×.files/image213.gif) =
=.files/image217.gif) ----------(14分)
----------(14分)
所有情况列表(仅供参考)
ξ
x
x
ξ=1
-1
-1-1+1-1+1
+1
-1-1+1-1+1
-1-1+1+1-1
-1-1+1+1-1
-1+1-1-1+1
-1+1-1-1+1
-1+1-1+1-1
-1+1-1+1-1
-1+1+1-1-1
-1+1+1-1-1
+
+
+
+
+1-1+
+1-1+
+1+
+1+
ξ=3
-3
+
+3
-1+1+1+1+1
-1+1-1-1-1
+1-1+1+1+1
-1-1+1-1-1
+1+1-1+1+1
-1-1-1
+1+1+1
19、(本小题满分14分)
.files/image218.jpg) 解:(I)∵
解:(I)∵.files/image220.gif) ∴
∴.files/image222.gif) ∴
∴.files/image224.gif)
∴.files/image226.gif) ………3分
………3分
∴.files/image228.gif) ………………………………4分
………………………………4分
设.files/image230.gif) ∴
∴.files/image232.gif)
.files/image234.gif) ∴
∴.files/image236.gif) …………………………………………6分
…………………………………………6分
∴.files/image238.gif) ……………………………………………………………………7分
……………………………………………………………………7分
(II)∵.files/image240.gif) ,
,.files/image236.gif) ………………………………………………………8分
………………………………………………………8分
∴.files/image242.gif) …………………………………………………………………9分
…………………………………………………………………9分
∴.files/image244.gif) …………………………………………………………10分
…………………………………………………………10分
由.files/image246.gif) ……………………12分
……………………12分
.files/image248.gif) …………………………………………………………14分
…………………………………………………………14分
∴直线EF与抛物线相切。
20.(本小题满分14分)
解:(1)∵x,y.files/image250.gif)
令.files/image252.gif) 为恒为零
为恒为零
∴.files/image254.gif)
令.files/image256.gif)
∴.files/image258.gif)
显然.files/image260.gif)
又函数.files/image132.gif) 为单调函数,可得
为单调函数,可得.files/image262.gif) 为等差数列
为等差数列
∴.files/image264.gif) 从而
从而.files/image266.gif) ---------------------------------------------------------(6分)
---------------------------------------------------------(6分)
(2)∵.files/image268.gif)
∴.files/image270.gif)
.files/image272.gif) 是递增数列。--------------------------------(12分)
是递增数列。--------------------------------(12分)
当.files/image274.gif) 时,
时,.files/image276.gif) ------------------------------------------------------(14分)
------------------------------------------------------(14分)
21、(本小题满分14分)
解:(1)由已知得函数.files/image278.gif) ,且
,且.files/image280.gif)
当.files/image282.gif) 又∵
又∵.files/image284.gif)
当.files/image286.gif)
∴函数.files/image288.gif) 的单调递增区间是
的单调递增区间是.files/image290.gif)
(2)设.files/image292.gif) ,
,
则.files/image294.gif) (5分)
(5分)
当.files/image296.gif)
又.files/image298.gif) 上连续,
上连续,.files/image300.gif) 内是增函数。(7分)
内是增函数。(7分)
.files/image302.gif) (8分)
(8分)
.files/image304.gif) (9分)
(9分)
.files/image306.gif) (10分)
(10分)
(3)方法一由(1)知,设.files/image308.gif)
将.files/image310.gif) ……12分
……12分
即.files/image312.gif)
.files/image314.gif) (14分)
(14分)
.files/image316.gif) 内是增函数。
内是增函数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com