题目列表(包括答案和解析)
（本小题满分12分）
(文科做)
某商场进行促销活动，促销方案是：顾客每消费100元，便可以获得奖券一张，每张奖券中奖的概率为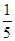
，若中奖，则商场返还顾客现金100元某顾客购买价格为340元的商品，得到3张奖券（I）求商场恰好返还该顾客现金100元的概率；
（II）求商场至少返还该顾客现金100元的概率.
（本小题满分12分）
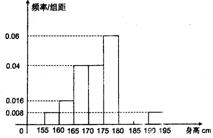
从某学校高三年级共800名男生中随机抽取50名测量身高，测量发现被测学生身高全部介于155 cm 和195 cm之间，将测量结果按如下方式分成八组：第一组[155,160)、第二组[160,165)、…、第八组[190,195]，下图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．
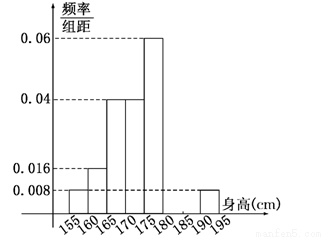
(1)估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数；
(2)求第六组、第七组的频率并补充完整频率分布直方图；
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为x、y，求满足|x－y|≤5的事件概率．
（本小题满分12分）甲、乙两队进行七局四胜制的比赛，即甲队或乙队谁先累计获胜四局比赛，即为冠军，若在每局比赛中，甲队获胜的概率为
，每局比赛必分出胜负，且每局比赛的胜负不影响下局的比赛。
求（1）在第5局比赛结束后决出冠军的概率？
（2）甲队获得冠军的概率？
(本小题满分12分) 某汽车驾驶学校在学员结业前，对学员的驾驶技术进行4次考核，规定：按顺序考核，一旦考核合格就不必参加以后的考核，否则还需参加下次考核。若学员小李独立参加每次考核合格的概率依次组成一个公差为
的等差数列，他参加第一次考核合格的概率不超过
，且他直到第二次考核才合格的概率为
。 1）求小李第一次参加考核就合格的概率
； 2）求小李参加考核的次数
的分布列和数学期望。
（本小题满分12分）从某学校高三年级共800名男生中随机抽取50名测量身高，据测量被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组
、第二组
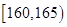；…第八组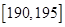
，右图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．
（I）求第六组、第七组的频率并补充完整频率分布直方图；
（II）若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为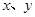
，求满足
的事件概率；
（III）从最后三组中任取3名学生参加学校篮球队，用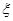
表示从第八组中取到的人数，求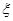的分布列及其数学期望。
一、选择题：每小题5分，共60分．
BDCBB DCBCB AA
二、填空题：每小题４分，共16分．
13. 300 14.（文）
，（理）3。 ⒖
⒗①③④.
三、解答题：
17．解：（Ⅰ）∵ 
=（sinB，1－cosB) , 且与向量
=（2，0）所成角为
∴
，∴ tan = ， 又∵ 0<B<p Þ 0< < ，
∴ = ，∴ B = 。
（Ⅱ）由（1）可得A + C = ，
∴
， 8分
∵
，∴
， 10分，∴
，
，当且仅当
。 12分
18.(文科))解：设既会唱歌又会跳舞的有x人，则文娱队中共有（7-x）人，那么只会一项的人数是（7-2 x）人． (I)∵
，∴
．
即
,∴
．∴x=2． 故文娱队共有5人．(8分)
(II) 
.(12分)
(理科)解:(Ⅰ) 甲得66分(正确11题)的概率为
,……2分
乙得54分(正确9题)的概率为
,……4分
显然
，即甲得66分的概率与乙得54分的概率一样大. ……6分
(Ⅱ)设答错一题倒扣x分，则学生乙选对题的个数为
随机选择20个题答对题的个数的期望为
,得分为
,
,令
,得
,
即每答错一题应该倒扣2分 ……12分
19．解：（Ⅰ）取BD中点N.连AN、MN.
就是异面直线AM与BC所成的角，在
中，
（4分）
（Ⅱ）取BE中点P.连AP、PM,作
于
过
作
于
连MH.
，
，即
AB 
的平面角，在
AMP中，
在ABP中，
二面角
的大小，为
（8分）
（Ⅲ）若将图(1)与图(2)面ACD重合，该几何体是5面体
这斜三棱柱的体积=3VA-BCD=3´
´
´
=
（12分）
20．（文科） (Ⅰ) ∵－(y＋3ax)＋(x3－1)＝0，∴＝(y＋3ax)－(x3－1)
∴(y＋3ax)＋[－(x3－1)]＝1，即y＝f(x)＝x3－3ax………………………2分
∴f/(x)＝3x2－
当a≤0时，f/(x)＝3(x2－a)≥0对x∈R恒成立，f(x)的单调区间为(－∞，＋∞)
当a＞0时，f/(x)＞0，x＜－或x＞
f/(x)＜0得－＜x＜…………………………………………6分
此时，函数f(x)在(－∞，－)和(，＋∞)上是增函数，
在(－，)上是减函数……………………………………8分
(Ⅱ)∵a＝1，∴f/(x)＝3x2－3，直线4x＋y＋m＝0的斜率为－4………………9分
假设f/(x)＝－4，即3x2＋1＝0无实根
∴直线4x＋y＋m＝0不可能是函数f(x)图象的切线………………………………12分
（理科）(Ⅰ)∵－[y＋
由于A、B、C三点共线 即[y＋
∴y＝f(x)＝ln(x＋1)＋1－
f /(x)＝，得f /(1)＝，故f(x)＝ln(x＋1)…………………………………4分
（Ⅱ）令g(x)＝f(x)－，由g/(x)＝－＝
∵x＞0，∴g/(x)＞0，∴g(x)在(0，＋∞)上是增函数………………6分
故g(x)＞g(0)＝0
即f(x)＞………………………………………………………………8分
（Ⅲ）原不等式等价于x2－f(x2)≤m2－2bm－3
令h(x)＝x2－f(x2)＝x2－ln(1＋x2)，由h/(x)＝x－＝…………………10分
当x∈[－1，1]时，h(x)max＝0，∴m2－2bm－3≥0
令Q(b)＝m2－2bm－3，则
得m≥3或m≤－3……………12分
21.解：（I）由
因直线
相切
，故所求椭圆方程为
（II）当L与x轴平行时，以AB为直径的圆的方程：
当L与x轴平行时，以AB为直径的圆的方程：
由
即两圆相切于点（0，1）
因此，所求的点T如果存在，只能是（0，1）.事实上，点T（0，1）就是所求的点，证明如下。
当直线L垂直于x轴时，以AB为直径的圆过点T（0，1）
若直线L不垂直于x轴，可设直线L：
由
记点
、
∴TA⊥TB，即以AB为直径的圆恒过点T（0，1）,故在坐标平面上存在一个定点T（0，1）满足条件.
22．(文科)解：（I）∵
. ∴曲线
在点
处的切线ln的斜率为
.
∴切线ln的方程为
. （2分）
令
得 
，∴
.
依题意点
在直线上，∴
又
. （4分）
∴数列
是1为首项，
为公比的等比数列. ∴
. （5分）
（Ⅱ）由已知
.
∴
.
①
. ②
①―②得
. （9分）
∴
（10分）
又
时，
.
又当
时，
. ∴
.∴当
时，
.
∴
∴
. （13分）综上
. （14分）
22．(理科)解： (Ⅰ)∵f(1)＝1，∴f(x)＝ea－1＝1 ∴a＝1 ……2分
(Ⅱ) x∈(0，1)时，f(x)＝xe
，
f＇(x)＝e＋xe(－2x＋a)＝(－2x2＋ax＋1)e,……3分
f＇(x)≥0
，
∵t（0）＝1∴－2x2＋ax＋1＞0在(0，1)恒成立Þ t (1) ≥
∴当a≥1时，f(x)在(0，1)上是增函数； ……5分
又当a＝1时，f(x)在(0，＋∞)也是单调递增的； ……6分
当a＞1时，∵
＝ea－1＞1=f(1)，此时，f(x)在(0，＋∞)不一定是增函数.…… 7分
(Ⅲ)当x∈(0，1)时，g(x)＝lnf(x)＋x2－ax＝lnx，当n≥2时，
欲证：－＜nk＝1－n，
即证－1－2－3－……－(n－1)＜ln＜1＋＋＋……＋－n
即需证
－1－2－3－……－(n－1)＜ln1＋ln＋ln＋……＋ln＜1＋＋＋……＋－n
猜想1－＜lnt＜t－1(其中0＜t＜1).……8分
构造函数h(t)＝lnt－1＋(0＜t＜1)
∵h＇(t)＝－＝＜0，∴h(t)在(0，1)上时单调递减的，
∴h(t)＞h（1）=0，即有lnt＞1－……10分
设s(t)＝lnt－t＋1(0＜t＜1)，
同理可证s(t)＜0，∴1－＜lnt＜t－1(0＜t＜1)成立 ……12分
分别取t＝，，……，(n≥2)，所得n－1个不等式相加即得：
－1－2－3－…－(n－1)＜ln1＋ln＋ln＋……＋ln＜1＋＋＋……＋－n
∴－＜nk＝1－n ……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com