
题目列表(包括答案和解析)
(本题满分16分,其中第(1)小题4分,第(2)小题8分,第(3)小题4分)
设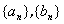 是两个数列,
是两个数列, 为直角坐标平面上的点.对
为直角坐标平面上的点.对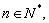 若三点
若三点 共线,
共线,
(1)求数列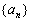 的通项公式;
的通项公式;
(2)若数列{ }满足:
}满足: ,其中
,其中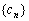 是第三项为8,公比为4的等比数列.求证:点列
是第三项为8,公比为4的等比数列.求证:点列 (1,
(1,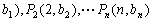 在同一条直线上;
在同一条直线上;
(3)记数列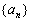 、{
、{ }的前
}的前 项和分别为
项和分别为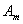 和
和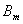 ,对任意自然数
,对任意自然数 ,是否总存在与
,是否总存在与 相关的自然数
相关的自然数 ,使得
,使得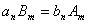 ?若存在,求出
?若存在,求出 与
与 的关系,若不存在,请说明理由.
的关系,若不存在,请说明理由.
给出下列四个函数:①f(x)=lnx;②f(x)=x2+1;③f(x)=e-x;④f(x)=sinx,其中满足:“对任意x1、x2∈(1,2),x1≠x2,不等式|f(x1)-f(x2)|<|x1-x2|总成立”的是________.(将正确的序中与填在横线上)
我们知道,如果定义在某区间上的函数![]() 满足对该区间上的任意两个数
满足对该区间上的任意两个数![]() 、
、![]() ,
,
总有不等式![]() 成立,则称函数
成立,则称函数![]() 为该区间上的向上凸函数(简称上凸).
为该区间上的向上凸函数(简称上凸).
类比上述定义,对于数列![]() ,如果对任意正整数
,如果对任意正整数![]() ,总有不等式:
,总有不等式:![]() 成立,
成立,
则称数列![]() 为向上凸数列(简称上凸数列). 现有数列
为向上凸数列(简称上凸数列). 现有数列![]() 满足如下两个条件:
满足如下两个条件:
(1)数列![]() 为上凸数列,且
为上凸数列,且![]() ;
;
(2)对正整数![]() (
(![]() ),都有
),都有![]() ,其中
,其中![]() .
.
则数列![]() 中的第五项
中的第五项![]() 的取值范围为 ★ .
的取值范围为 ★ .
我们知道,如果定义在某区间上的函数![]() 满足对该区间上的任意两个数
满足对该区间上的任意两个数![]() 、
、![]() ,总有不等式
,总有不等式![]() 成立,则称函数
成立,则称函数![]() 为该区间上的向上凸函数(简称上凸). 类比上述定义,对于数列
为该区间上的向上凸函数(简称上凸). 类比上述定义,对于数列![]() ,如果对任意正整数
,如果对任意正整数![]() ,总有不等式:
,总有不等式:![]() 成立,则称数列
成立,则称数列![]() 为向上凸数列(简称上凸数列). 现有数列
为向上凸数列(简称上凸数列). 现有数列![]() 满足如下两个条件:
满足如下两个条件:
(1)数列![]() 为上凸数列,且
为上凸数列,且![]() ;
;
(2)对正整数![]() (
(![]() ),都有
),都有![]() ,其中
,其中![]() .
.
则数列![]() 中的第五项
中的第五项![]() 的取值范围为 ▲ .
的取值范围为 ▲ .
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| an+an+2 |
| 2 |
一、选择题 ABCBD DBCDC CC
二、填空题
13.6; ;14.
;14. ;15.
;15. ,1)∪(1,+∞);16。①③④
,1)∪(1,+∞);16。①③④
三、解答题
17. 解:(1)∵  , 且与向量
, 且与向量 所成角为
所成角为
∴  ,
∴
,
∴  ,
,
又 ,∴
,∴
 ,即
,即 。
。
(2)由(1)可得:
∴ 



∵  ,∴
,∴
 ,
,
∴  ,∴
当
,∴
当 =1时,A=
=1时,A=
∴AB=2, 则
18.解:(1)P=
(2)随机变量 的取值为0, 1, 2, 3.
的取值为0, 1, 2, 3.
由n次独立重复试验概率公式 得
得




随机变量 的分布列是
的分布列是

0
1
2
3





 的数学期望是
的数学期望是 
19.(I)解:取CE中点P,连结FP、BP,
∵F为CD的中点,∴FP//DE,且FP=
又AB//DE,且AB= ,∴AB//FP,且AB=FP,
,∴AB//FP,且AB=FP,
∴ABPF为平行四边形,∴AF//BP。…………2分
又∵AF 平面BCE,BP
平面BCE,BP 平面BCE,∴AF//平面BCE。
…………4分
平面BCE,∴AF//平面BCE。
…………4分
(II)∵△ACD为正三角形,∴AF⊥CD。
∵AB⊥平面ACD,DE//AB,∴DE⊥平面ACD,又AF 平面ACD,
平面ACD,
∴DE⊥AF。又AF⊥CD,CD∩DE=D,∴AF⊥平面CDE。 …………6分
又BP//AF,∴BP⊥平面CDE。又∵BP 平面BCE,
平面BCE,
∴平面BCE⊥平面CDE。 …………8分
(III)由(II),以F为坐标原点,FA,FD,FP所在的直线分别为x,y,z轴(如图),建立空间直角坐标系F―xyz.设AC=2,
则C(0,―1,0), ………………9分
………………9分
 ……10分
……10分
显然, 为平面ACD的法向量。
为平面ACD的法向量。
设平面BCE与平面ACD所成锐二面角为
 ,即平面BCE与平面ACD所成锐二面角为45°。…………12分
,即平面BCE与平面ACD所成锐二面角为45°。…………12分
20.(1)

 时,
时, ,即
,即
当 时,
时,
即
 在
在 上是减函数的充要条件为
上是减函数的充要条件为 ………(4分)
………(4分)
(2)由(1)知,当 时
时 为减函数,
为减函数, 的最大值为
的最大值为 ;
;
当 时,
时,
 当
当 时
时 ,当
,当 时
时
即在 上
上 是增函数,在
是增函数,在 上
上 是减函数,
是减函数, 时
时 取最大值,最大值为
取最大值,最大值为 即
即 …(8分)
…(8分)
(3)在(1)中取 ,即
,即
由(1)知 在
在 上是减函数
上是减函数
 ,即
,即
 ,解得:
,解得: 或
或
故所求不等式的解集为[ ……………(12分)
……………(12分)
21. 解:(1) ,
, ,
,
又 ,∴数列
,∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
(2)依(Ⅰ)的结论有 ,即
,即 .
.
 .
.
 .
.
(3) ,又由(Ⅱ)有
,又由(Ⅱ)有
 .
.
则
 (
(  ) =
) = 
=( 1- )<∴ 对任意的
)<∴ 对任意的 ,
, .
.
22.解:(I)由条件知: ………2分
………2分
得 ………4分
………4分
(II)依条件有: ………5分, 由
………5分, 由

 8分
8分

由 ,
, ………10分
………10分
由弦长公式得
由

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com