
题目列表(包括答案和解析)
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
20.在二项式 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列
(1)求展开式的常数项; (2)求展开式中二项式系数最大的项;
(3)求展开式中各项的系数和。
【解析】本试题主要考查了二项式定理中通项公式和二项式系数的概念以及求解各个系数和的运用,赋值法思想要深刻体会。
函数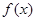 的定义域为
的定义域为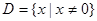 ,且满足对于任意
,且满足对于任意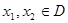 ,有
,有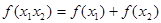 .
.
⑴求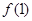 的值;
的值;
⑵判断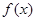 的奇偶性并证明;
的奇偶性并证明;
⑶如果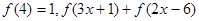 ≤
≤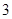 ,且
,且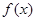 在
在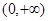 上是增函数,求
上是增函数,求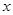 的取值范围.
的取值范围.
【解析】(Ⅰ) 通过赋值法,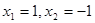 ,求出f(1)0;
,求出f(1)0;
(Ⅱ) 说明函数f(x)的奇偶性,通过令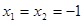 ,得
,得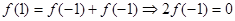 .令
.令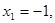
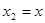 ,得
,得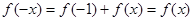 ,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
(Ⅲ) 推出函数的周期,根据函数在[-2,2]的图象以及函数的周期性,即可求满足f(2x-1)≥12的实数x的集合.
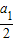
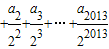 = .
= .| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com