
题目列表(包括答案和解析)
| k | 2t+1 |
为了提高产品的年产量,某企业拟在2013年进行技术改革.经调查测算,产品当年的产量 万件与投入技术改革费用
万件与投入技术改革费用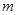 万元(
万元( )满足
)满足 (
( 为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的
为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的 倍(生产成本包括固定投入和再投入两部分资金).
倍(生产成本包括固定投入和再投入两部分资金).
(Ⅰ)试确定的 值,并将2013年该产品的利润
值,并将2013年该产品的利润 万元表示为技术改革费用
万元表示为技术改革费用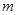 万元的函数(利润=销售金额―生产成本―技术改革费用);
万元的函数(利润=销售金额―生产成本―技术改革费用);
(Ⅱ)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?
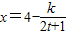 (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2010年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍,(产品成本包括固定投入和再投入两部分).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2010年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍,(产品成本包括固定投入和再投入两部分). (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2010年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍,(产品成本包括固定投入和再投入两部分).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2010年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍,(产品成本包括固定投入和再投入两部分).某厂家拟在2013年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与年促销费用
万件与年促销费用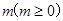 万元满足
万元满足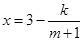 (
(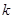 为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的
为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的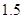 倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2013年该产品的利润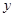 万元表示为年促销费用
万元表示为年促销费用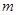 万元的函数;
万元的函数;
(2)该厂家2013年的促销费用投入多少万元时,厂家的利润最大?
一、选择题:(本大题10个小题,每小题5分,共50分)
1--5 BDDCA 6--10 ACBCB
二.填空题:(本大题共6小题,每小题4分,共24分)
 ;
12.
;
12. ; 13.
; 13.  ; 14.
; 14.  ;
;

 ;
;
三、解答题:(本大题共6小题,共76分).
17.(13分)
解:(I)
 ………………………(6分)
………………………(6分)
 函数
函数 的单调减区间为
的单调减区间为 ……………………(7分)
……………………(7分)
(II) 则
则
 ……………(11分)
……………(11分)
 函数
函数 的最大值为
的最大值为 ,最小值为
,最小值为 .…………………………(13分)
.…………………………(13分)
18.(13分)
解:(I) ①
①
 当
当 时,
时, ②
②
将①-②得 …………………(4分)
…………………(4分)
在①中,令 得
得
 ………………………………………………(6分)
………………………………………………(6分)
(II)由 得
得 则当
则当 时,
时, ………(8分)
………(8分)
 当
当 时,
时,  ……………………(9分)
……………………(9分)
则
 ……………(12分)
……………(12分)
又
 …………………………………………(13分)
…………………………………………(13分)
19.(13分)
解:(I)由题意有 ,得
,得 ,故
,故


(II)由(I)知:
 ……(11分)
……(11分)
当且仅当 即
即 时,
时, 有最大值.
有最大值.
答: 2009年的年促销费用投入2.5万元时,该厂家利润最大. …………(13分)
20.(13分)
解:(I) 时,
时, ,即
,即 (※)
(※)
(1)当 时,由(※)
时,由(※)
又 ,
, ………………………………………………(2分)
………………………………………………(2分)
(2)当 时,由(※)
时,由(※)
又 ,
, ………………………………………(4分)
………………………………………(4分)
(3)当 时,由(※)
时,由(※)
又 ,
, ………………………………………………(6分)
………………………………………………(6分)
综上:由(1)、(2)、(3)知原不等式的解集为 ……………(7分)
……………(7分)
(II)当 时,
时, ,即
,即 恒成立,
恒成立,
也即 在
在 上恒成立。…………………(10分)
上恒成立。…………………(10分)
而 在
在 上为增函数,故
上为增函数,故
 当且仅当
当且仅当 即
即 时,等号成立.
时,等号成立.
故 ………………………………………………… (13分)
………………………………………………… (13分)
21.(12分)
解:(I)在 中,由余弦定理得
中,由余弦定理得 (1分)
(1分)

 ………(4分)
………(4分)
 ,即动点
,即动点 的轨迹为以A、B为两焦点的椭圆.
的轨迹为以A、B为两焦点的椭圆.
 动点
动点 的轨迹
的轨迹 的方程为:
的方程为: .…………………………
(6分)
.…………………………
(6分)
(II)由 得
得 .(※)… (7分)
.(※)… (7分)
设 、
、 ,易知
,易知 ,则
,则 ①
①
 ②…………………………………………………(8分)
②…………………………………………………(8分)
又

 ③…………………………………………… (10分)
③…………………………………………… (10分)
将③代入①、②得 消去
消去 得
得 或
或
 ,代入(※)方程
,代入(※)方程 .故
.故 …………… (12分)
…………… (12分)
22.(12分)
解:(I)由 得
得
故 ………………………………(2分)
………………………………(2分)
(II)由 得
得

 …………(4分)
…………(4分)





从而 即
即
 …………………………………………………(6分)
…………………………………………………(6分)
(III )由 得
得
设 ,则
,则 且
且
于是 …………………………………(8分)
…………………………………(8分)
设 则
则 且
且

 ……………(10分)
……………(10分)
从而 时,
时,
当 时,
时,
 ……………………………………………(12分)
……………………………………………(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com