练习册

  • 练习册
  • 试题
    【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分15分）

    已知函数，其中， （），若相邻两对称轴间的距离不小于．

       （Ⅰ）求的取值范围；

       （Ⅱ）在中，分别是角的对边，，当最大时，，求的面积．

    查看答案和解析>>

    （本小题满分15分）

    某旅游商品生产企业，2009年某商品生产的投入成本为1元/件，

    出厂价为流程图的输出结果元/件，年销售量为10000件，

    因2010年国家长假的调整，此企业为适应市场需求，

    计划提高产品档次，适度增加投入成本．若每件投入成本增加的

    比例为（），则出厂价相应提高的比例为，

    同时预计销售量增加的比例为．

    已知得利润（出厂价投入成本）年销售量．

    （Ⅰ）写出2010年预计的年利润

    与投入成本增加的比例的关系式；

    （Ⅱ）为使2010年的年利润比2009年有所增加，

    问：投入成本增加的比例应在什么范围内？

    查看答案和解析>>

    （本小题满分15分）某地有三个村庄，分别位于等腰直角三角形ABC的三个顶点处，已知AB=AC=6km，现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.

    （1）设，把y表示成的函数关系式；

    （2）变电站建于何处时，它到三个小区的距离之和最小？

    查看答案和解析>>

    （本小题满分15分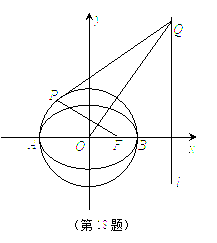）如图，已知圆O：x2+y2=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为的椭圆，其右焦点为F．若点P(－1,1)为圆O上一点，连结PF，过原点O作直线PF的垂线交椭圆C的右准线l于点Q．（1）求椭圆C的标准方程；

    （2）证明：直线PQ与圆O相切．

    查看答案和解析>>

    （本小题满分15分）已知等差数列{an}中，首项a1＝1，公差d为整数，且满足a1+3＜a3，a2+5＞a4，数列{bn}满足，其前n项和为Sn．（1）求数列{an}的通项公式an；（2）若S2为S1，Sm(m∈N*)的等比中项，求正整数m的值．

    查看答案和解析>>

    第Ⅰ部分（正卷）

    一、填空题：本大题共14小题，每小题5分，计70分。

    1、    2、    3、对任意使    4、2    5、

    6、    7、    8、8      9、        10、40

    11、    12、4       13、    14、

    二、解答题：本大题共6小题，计90分。解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内。

    15、解：（1）解：，

    由，有，

    解得。                                         ……7分

    （2）解法一：       ……11分

                 。  ……14分

      解法二：由（1），，得

    ∴   

    ∴                                        ……10分

    于是，

                   ……12分

    代入得。            ……14分

    16、证明：（1）∵

    ∴                                          ……4分

    （2）令中点为，中点为，连结、

         ∵是的中位线

    ∴           ……6分   

    又∵

    ∴

    ∴     ……8分

         ∴

         ∵为正

    ∴         ……10分

         ∴

         又∵，

     ∴四边形为平行四边形    ……12分

    ∴

    ∴    ……14分

    17、解：（1）设米，，则

    ∵

    ∴

    ∴                                                ……2分

    ∴

    ∴                                            ……4分

    ∴

    ∴或                                            ……5分

    （2）                   ……7分

          

         

         此时                                               ……10分

    （3）∵

    令，                       ……11分

    ∵

    当时，

    ∴在上递增                       ……13分

    ∴

    此时                                                ……14分

    答：（1）或

        （2）当的长度是4米时，矩形的面积最小，最小面积为24平方米；

        （3）当的长度是6米时，矩形的面积最小，

    最小面积为27平方米。                              ……15分

    18、（1）解：①若直线的斜率不存在，即直线是，符合题意。   ……2分

    ②若直线斜率存在，设直线为，即。

    由题意知，圆心以已知直线的距离等于半径2，即：，

    解之得                                                  ……5分

    所求直线方程是，                            ……6分

    （2）解法一：直线与圆相交，斜率必定存在，且不为0，可设直线方程为

    由得                       ……8分

    又直线与垂直，由得 ……11分

    ∴

    ……13分

                 为定值。

       故是定值，且为6。                            ……15分

    19、解：（1）由题意得，                             ……2分

    ∴，    ∴    ……3分

    ∴，∴在是

    单调增函数，                                             ……5分

    ∴对于恒成立。      ……6分

    （2）方程；   ∴  ……7分

         ∵，∴方程为                      ……9分

         令，，

          ∵，当时，，∴在上为增函数；

         时，，  ∴在上为减函数，    ……12分

         当时，                     ……13分

    ，            

    ∴函数、在同一坐标系的大致图象如图所示，

    ∴①当，即时，方程无解。

    ②当，即时，方程有一个根。

    ③当，即时，方程有两个根。    ……16分

     

     

     

     

     

     

     

     

    第Ⅱ部分（附加卷）

    一、必做题

    21、解：（1）由得，

    求得，，                                ……3分

    (2)猜想                                            ……5分

    证明：①当时，猜想成立。                                 ……6分

    ②设当时时，猜想成立，即，          ……7分

    则当时，有,

    所以当时猜想也成立                                  ……9分

    ③综合①②，猜想对任何都成立。                      ……10分

    22、解：（1）“油罐引爆”的事件为事件A，其对立事件，则

    ∴ 答：油罐被引爆的概率为 ……5分

    （2）射击次数的可能取值为2，3，4，5，

    ，，

    ，   ……7分

    故的分布列为：

    2

    3

    4

    5

    P

         ……10分

    二、选做题（每题10分）（选两道）

    1、证明：因为A，M，D，N四点其圆，

      所以，              ……3分

    同理，有         ……5分

    所以，   ……7分 

    即，

    所以  ……10分

    2、解：（1）设A的一个特值为，由题意知：

      =0

    ，          ……2分

    当时，由 ，得A属于特征值2的特征向量

    当时，由

    同步练习册答案