
题目列表(包括答案和解析)
 (2012•蓝山县模拟)某公园的大型中心花园的边界为椭圆,花园内种植各种花草,为增强观赏性,在椭圆内以其中心为直角顶点且关于中心对称的两个直角三角形内种植名贵花草(如图),并以该直角三角形斜边开辟观赏小道(不计小道的宽度),某园林公司承接了该中心花园的施工建设,在施工时发现,椭圆边界上任意一点到椭圆两焦点距离和为4(单位:百米),且椭圆上点到焦点的最近距离为1(单位:百米).
(2012•蓝山县模拟)某公园的大型中心花园的边界为椭圆,花园内种植各种花草,为增强观赏性,在椭圆内以其中心为直角顶点且关于中心对称的两个直角三角形内种植名贵花草(如图),并以该直角三角形斜边开辟观赏小道(不计小道的宽度),某园林公司承接了该中心花园的施工建设,在施工时发现,椭圆边界上任意一点到椭圆两焦点距离和为4(单位:百米),且椭圆上点到焦点的最近距离为1(单位:百米).
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示. 其上部分是以 为直径的半圆,点
为直径的半圆,点 为圆心,下部分是以
为圆心,下部分是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,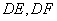 是两根支杆,其中
是两根支杆,其中 米,
米, .
现在弧
.
现在弧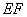 、线段
、线段 与线段
与线段 上装彩灯,在弧
上装彩灯,在弧 、弧
、弧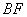 、线段
、线段 与线段
与线段 上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为
上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为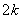 ,节能灯的比例系数为
,节能灯的比例系数为 ,假定该霓虹灯整体的“心悦效果”
,假定该霓虹灯整体的“心悦效果” 是所有灯“心悦效果”的和.
是所有灯“心悦效果”的和.
(Ⅰ)试将 表示为
表示为 的函数;
的函数;
(Ⅱ)试确定当 取何值时,该霓虹灯整体的“心悦效果”最佳?
取何值时,该霓虹灯整体的“心悦效果”最佳?

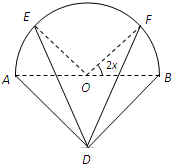 某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示.其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE,DF是两根支杆,其中AB=2米,∠EOA=∠FOB=2x(0<x<
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示.其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE,DF是两根支杆,其中AB=2米,∠EOA=∠FOB=2x(0<x<| π | 4 |
(1)一张大馅饼的概率;
(2)一张中馅饼的概率;
(3)一张小馅饼的概率;
(4)得不到馅饼的概率.(精确到小数点后两位)
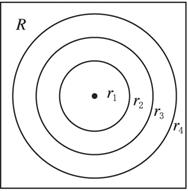
(意大利馅饼问题)山姆的意大利馅饼屋中设有一个投镖靶.该靶为正方形板,边长为18厘米,挂于前门附近的墙上,顾客花两角五分的硬币便可投一镖,并有机会赢得一种意大利馅饼中的一个.投镖靶中画有三个同心圆,圆心在靶的中心,当镖击中半径为1厘米的最内层圆形区域时,可得到一个大馅饼;当镖击中半径为1厘米到2厘米之间的环形区域时,可得到一个中馅饼;当镖击中半径为2厘米到3厘米之间的环形区域时,可得到一个小馅饼;如果镖击中靶上的其他部分,则得不到馅饼.假设每一位顾客都能投镖中靶,并且每个圆的周边线没有宽度,即每个镖不会击在线上,试求一位顾客赢得下列各种馅饼的概率:
(1)一个大馅饼;(2)一个中馅饼;(3)一个小馅饼;(4)没得到馅饼.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com