
题目列表(包括答案和解析)
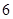 位选手依次演讲,其中选手甲不再第一个也不再最后一个演讲,则不同的演讲次序共有
位选手依次演讲,其中选手甲不再第一个也不再最后一个演讲,则不同的演讲次序共有
(A)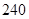 种 (B)
种 (B)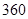 种
(C)
种
(C)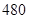 种 (D)
种 (D)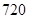 种
种
【解析】先排甲,有4种方法,剩余5人全排列有 种,所以不同的演讲次序有
种,所以不同的演讲次序有 种,选C.
种,选C.
已知集合A={(x,y)|x2+y2=4},B={(x,y)|x2+y2=1},则A、B的关系为【 】.
A. ![]() B.
B. ![]() C.
C. ![]() D. A∩B=
D. A∩B=![]()
【解析】A.设![]()
![]() ,所以
,所以![]() 是偶函数,所以选A.
是偶函数,所以选A.
设数列{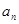 }的前n项和
}的前n项和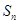 满足:
满足: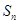 =n
=n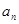 -2n(n-1).等比数列{
-2n(n-1).等比数列{ }的前n项和为
}的前n项和为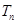 ,公比为
,公比为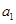 ,且
,且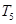 =
=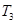 +2
+2 .
.
(1)求数列{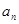 }的通项公式;
}的通项公式;
(2)设数列{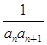 }的前n项和为
}的前n项和为 ,求证:
,求证: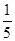 ≤
≤ <
<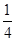 .
.
【解析】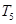 =
=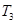 +2
+2 求出
求出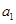 ,由
,由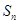 =n
=n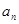 -2n(n-1)递写一个式子相减,得{
-2n(n-1)递写一个式子相减,得{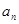 }为等差数列;(2)裂项法求
}为等差数列;(2)裂项法求 ,然后证明
,然后证明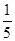 ≤
≤ <
<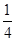 .
.
已知集合A={(x,y)|x2+y2=4},B={(x,y)|x2+y2=1},则A、B的关系为【 】.
A. 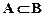 B.
B. 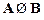 C.
C. 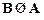 D. A∩B=
D. A∩B=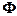
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com