
题目列表(包括答案和解析)
在数列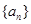 中,
中,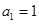 ,当
,当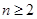 时,
时,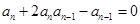
(Ⅰ)求数列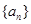 的通项公式;
的通项公式;
(Ⅱ)设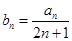 ,求数列
,求数列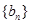 的前
的前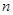 项和
项和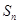 .
.
【解析】本试题主要考查了数列的通项公式的求和 综合运用。第一问中 ,利用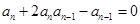 ,得到
,得到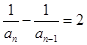 且
且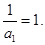 ,故故
,故故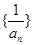 为以1为首项,公差为2的等差数列. 从而
为以1为首项,公差为2的等差数列. 从而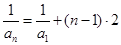

第二问中,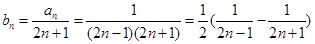
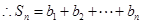
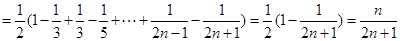
由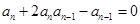 及
及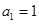 知
知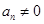 ,从而可得
,从而可得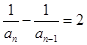 且
且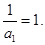
故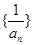 为以1为首项,公差为2的等差数列.
为以1为首项,公差为2的等差数列.
从而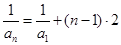
 ……………………6分
……………………6分
(2)
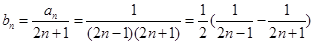 ……………………9分
……………………9分
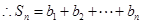
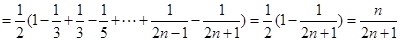
设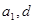 为实数,首项为
为实数,首项为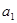 ,公差为
,公差为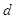 的等差数列
的等差数列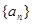 的前n项和为
的前n项和为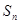 ,满足
,满足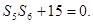
(1)若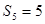 ,求
,求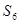 及
及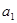 ;
;
(2)求d的取值范围.
【解析】本试题主要考查了数列的求和的运用以及通项公式的运用。第一问中,利用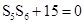 和已知的
和已知的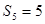 ,得到结论
,得到结论
第二问中,利用首项和公差表示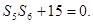 ,则方程是一个有解的方程,因此判别式大于等于零,因此得到d的范围。
,则方程是一个有解的方程,因此判别式大于等于零,因此得到d的范围。
解:(1)因为设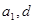 为实数,首项为
为实数,首项为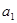 ,公差为
,公差为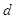 的等差数列
的等差数列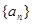 的前n项和为
的前n项和为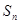 ,满足
,满足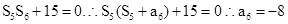
所以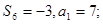
(2)因为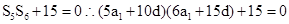
得到关于首项的一个二次方程,则方程必定有解,结合判别式求解得到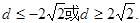
已知 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)记 ,
, ,证明
,证明 (
( ).
).
【解析】(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q.
由 ,得
,得 ,
, ,
, .
.
由条件,得方程组 ,解得
,解得
所以 ,
, ,
, .
.
(2)证明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:数学归纳法)
① 当n=1时,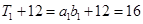 ,
, ,故等式成立.
,故等式成立.
② 假设当n=k时等式成立,即 ,则当n=k+1时,有:
,则当n=k+1时,有:






即 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立
由①和②,可知对任意 ,
, 成立.
成立.
已知数列 是公差不为零的等差数列,
是公差不为零的等差数列,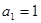 ,且
,且 、
、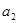 、
、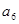 成等比数列。
成等比数列。
⑴求数列 的通项公式;
的通项公式;
⑵设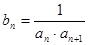 ,求数列
,求数列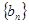 的前
的前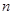 项和
项和 。
。
【解析】第一问中利用等差数列 的首项为
的首项为 ,公差为d,则依题意有:
,公差为d,则依题意有:
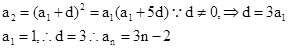
第二问中,利用第一问的结论得到数列的通项公式,
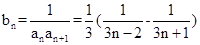 ,利用裂项求和的思想解决即可。
,利用裂项求和的思想解决即可。
如图,有三个并排放在一起的正方形,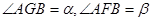 .
.
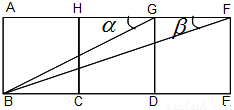
(1)求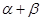 的度数;
的度数;
(2)求函数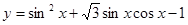 的最大值及取得最大值时候的x值。
的最大值及取得最大值时候的x值。
【解析】本试题主要是考查了三角函数的两角和差的三角公式的运用以及三角函数性质的综合运用。
(1)妨设正方形边长为1,易知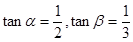 ,可得
,可得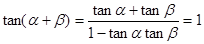 得到结论。
得到结论。
(2)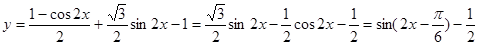 可知y的最大值,进而得到x的取值集合。
可知y的最大值,进而得到x的取值集合。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com