
题目列表(包括答案和解析)
A同学利用下列方法测量B同学的反应:A同学拿著一把有刻度的直尺,其中直尺成垂,零刻度在下端。B同学手指靠近直尺下端(16)。在有提出警告的情下,A同学释放直尺B同学尽快用手指住直尺。果显示B同学着直尺位置的刻度 45 cm (17)。(取g=10m/s2)
|
|


16 17
(1)计算B同学的反应 (4分)
(2) 若改用一把重的直尺行以上,果有何影响?用重力公式及牛顿第二定律加以解释。 (4分)
(3)古希腊哲学家亚里士多德最早认为,物体下落的快慢是由它们的重量大小决定的,物体越重,下落得越快,但是物理学家伽利略用简单明了的科学推理,巧妙地揭示了亚里士多德的理论内容包含的矛盾.指出:根据亚里士多德的论断,一块大石头的下落速度要比一块小石头的下落速度大,假定大石头下落速度为8,小石头下落的速度为4,当我们把石头拴在一起时,下落快的会被下落慢的拖着而减慢,下落慢的会被下落快的拖着而加快,结果整体系统的下落速度应该小于8.但是两块石头拴在一起,加起来比大石头还要重,根据亚里士多德的理论,整个系统的下落速度应该大于8.这样就使得亚里士多德的理论陷入了自相矛盾的境地.伽利略由此推断重的物体不会比轻的物体下落得快.根据伽利略的推理方法,假设用两块同样重的石头为研究对象,你又如何推翻亚里士多德的结论呢?(回答应简明)(4分)
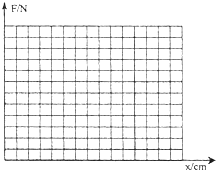 以下是一位同学探究“弹力与形变的关系”的实验,他按以下步骤完成了正确的操作:
以下是一位同学探究“弹力与形变的关系”的实验,他按以下步骤完成了正确的操作:| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15.0 | 15.0 | 15.0 | 15.0 | 15.0 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) | 1.2 1.2 |
2.3 2.3 |
3.5 3.5 |
4.6 4.6 |
5.8 5.8 |
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15.0 | 15.0 | 15.0 | 15.0 | 15.0 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) | ______ | ______ | ______ | ______ | ______ |

(6分)以下是一位同学做“探究形变与弹力的关系”的实验。
a.下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来是: 。
A、以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来。
B、记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C、将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D、依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E、以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.
F、解释函数表达式中常数的物理意义.
b.下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15 | 15 | 15 | 15 | 15 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) | 1.2 | 2.3 | 3.5 | 4.6 | 5.8 |
![]() 在下图的坐标上作出F-x图线。
在下图的坐标上作出F-x图线。
②写出曲线的函数表达式(x用cm作单位):
③函数表达式中常数的物理意义:
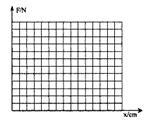
以下是一位同学做“探究形变与弹力的关系”的实验。
a.下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来是: 。
A、以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来。
B、记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C、将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D、依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E、以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.
F、解释函数表达式中常数的物理意义.
b.下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15 | 15 | 15 | 15 | 15 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) | 1.2 | 2.3 | 3.5 | 4.6 | 5.8 |
1在下图的坐标上作出F-x图线。
 ②写出曲线的函数表达式(x用cm作单位):
②写出曲线的函数表达式(x用cm作单位):
③函数表达式中常数的物理意义:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com