题目列表(包括答案和解析)
用多用电表测量阻值约十几千欧的电阻Rx。S为电表的选择开关，P为欧姆挡调零旋钮。
①从以下给出的操作步骤中，选择必要的步骤，并排出合理顺序：____________。
（填步骤前的字母）
A．旋转s至欧姆挡“×lk”
B．旋转s至欧姆挡“×100”
C．旋转S至“OFF”，并拔出两表笔
D．将两表笔分别连接到Rx，的两端，
读出阻值后，断开两表笔
E．将两表笔短接，调节P使指针对准刻度盘上欧姆挡的零刻度，断开两表笔
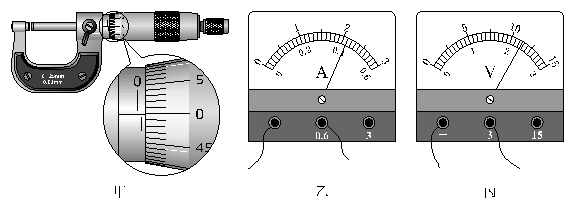
② 按正确步骤测量时，指针指在图示位置，Rx的测量值为__________ kΩ。
（2）某实验小组在“测定金属电阻率”的实验过程中，正确操作获得金属丝的直径以及电流表、电压表的读数如图所示，则它们的读数值依次是_________、________、__________。
已知实验中所用的滑动变阻器阻值范围为0~10Ω，电流表内阻约几欧，电压表内阻约20kΩ。电源为干电池（不宜在长时间、大功率状况下使用），电动势E = 4.5V，内阻很小。则以下电路图中__________（填电路图下方的字母代号）电路为本次实验应当采用的最佳电路。但用此最佳电路测量的结果仍然会比真实值偏_________。
若已知实验所用的电流表内阻的准确值
，那么准确测量金属丝电阻
的最佳电路应是上图中的__________电路（填电路图下的字母代号）。此时测得电流为I、电压为U，则金属丝电阻
___________（ 用题中字母代号表示）。
|
（1）用多用电表测量阻值约十几千欧的电阻Rx．S为电表的选择开关，P为欧姆挡调零旋钮．
| L（m） | 0.9956 | 0.8049 | 0.5981 | 0.4021 | 0.1958 |
| R（Ω） | 104.8 | 85.3 | 65.2 | 46.6 | 27.1 |
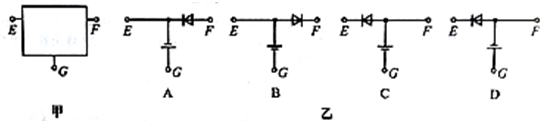
（17分）（1）①用多用电表探测图甲所示黑箱发现：用直流电压挡测量，E、G两点间和F、G两点间均有电压，E、F两点间无电压；用欧姆测量，黑表笔（与电表内部电源的正极相连）接E点，红表笔（表电表内部电源的负极相连）接F点，阻值很小，但反接阻值很大。那么，该黑箱内元件的接法可能是图乙中 。
[来源:Z,xx,k.Com]
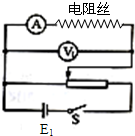
②在物理兴趣小组活动中，一同学利用下列器材设计并完成了“探究导体阻值与长度的关系”的实验。
电压表
量程3V 内阻约为900
电压表
量程10V 内阻约为3K
电压表
量程60mA 内阻约为5[来源:学科
电源E1 电动势1.5V 内阻约为0.2
电源E2 电动势4.5V 内阻约为0.4
滑动变阻器（最大阻值为10
）。粗细均匀的同种电阻丝，开关、导线和刻度尺
其主要实验步骤如下：
A.选取图中器材，按示意图连接电路
B.用伏安法测定电阻丝的阻值R
C.用刻度尺没出电阻丝的长度L
D.依次减小电阻丝的长度，保持电路其他部分不变，重复步骤B、C[来源:学.科.网Z.X.X.K][来源:学#科#网Z#X#X#K]
E.处理数据，根据下列测量结果，找出电阻丝值与长度的关系
| L(m) | 0.9956 | 0.8049 | 0.5981 | 0.4021 | 0.1958 |
| R( | 104.8 | 85.3 | 65.2 | 46.6 | 27.1 |
为使实验尽可能准确，请你对上述步骤中画线处加以改进。
（I）
（II）
（2）有4条用打点计时器（所用交流电频率为50Hz）打出的纸带A、B、C、D，其中一条是做“验证机械能守恒定律”实验时打出的。为找出该纸带，某同学在每条纸带上取了点迹清晰的、连续的4个点，用刻度尺测出相邻两个点间距离依次为S1、S2、S3。请你根据下列S1、S2、S3的测量结果确定该纸带为 。（已知当地的重力加速度为9.791m/s2）
A.61.0mm 65.8mm 70.7mm B. 41.2mm 45.1mm 53.0mm
C.4936mm 53.5mm 57.3mm D. 60.5mm 61.0mm 60.6mm
一、1―5BCBAD 6―10BDACB 11―13DAC
二、14．BC 15．B 16．AC 17．B 18．C 19．C 20．BD 21．B
三、
22．（I）（每空2分，共6分） 左 1.60 9.60（9.6）
（II）（每问4分，共12分）①乙
②A：按乙图连接好实验电路；B：闭合s1、s2，记下电压表的读数U1；C：再断开s2，记下电压表的读数U2 （4分，B项和C项步骤各2分）
③
（4分）
23．（14分）解：（1）设乙在接棒前跑过的路程为s1，
由运动学公式得
① （3分）
设乙启动到最大速度过程中，跑过的路程为s，
由运动学公式得
② （3分）
由①②得s1=
（2）设甲、乙交棒之前，甲跑过的路程为s2，
有
③ （2分）
在此过程中，对乙分析有
④ （2分）
由②③④得s2=
则甲乙相距△s=s2-s1=
24．（19分）解：（1）对B球:从静止释放至摆到最低点过程中，根据动能定理，有
① （4分）
代入数据，解得B球在最低点的速率 v=
（2） B球与A球碰撞过程中，两球所组成的系统动量守恒，动能不损失，取水平向右为正方向，有
② （2分）
③
（2分）
联立②、③，解得B球速度v1=
A球速度为v2=
根据电荷守恒定律得，碰后A球带电量
（1分）
A球离开平台后，由牛顿第二定律得
④ （2分）
故竖直方向的加速度
（1分）
A球从离开平台至着地过程中，
由
得
（1分）
水平位移大小S=v2t=2×
25．（21分）解：（1）设水平拉力为F ，
则
① （1分）
对框架由牛顿第二定律得
② （2分）
解得
（1分） ]
（2）设框架做匀速运动的速度大小为v，
则感应电动势
③ （2分）
回路中的电流 
④ （2分）
对框架由力的平衡得
⑤ （2分）
联立上式解得
（1分）
（3）在框架滑过s的过程中，设产生的电热为Q1 ，摩擦生热为Q2
由功能关系得
⑥ （3分）
其中
⑦ （2分）
在框架匀速运动后，对棒由力的平衡得
⑧ （2分）
另有
⑨ （1分）
联立以上各式得
（2分）
|
（3分） 
（2） CH3COOH＋C2H5OH CH3COOC2H5＋H2O （2分）
