
题目列表(包括答案和解析)
数列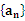 的前n项和为Sn,已知a15,且nSn+12n(n+1)+(n+1)Sn(
的前n项和为Sn,已知a15,且nSn+12n(n+1)+(n+1)Sn(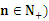 ,则与过点P(n,an)和点Q(n+2,an+1) (
,则与过点P(n,an)和点Q(n+2,an+1) (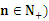 的直线平行的向量可以是 ( )
的直线平行的向量可以是 ( )
| A.(1 , 2) | B.(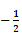 , 2) , 2) | C.(2 ,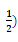 | D.(4 , 1) |
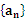 的前n项和为Sn,已知a15,且nSn+12n(n+1)+(n+1)Sn(
的前n项和为Sn,已知a15,且nSn+12n(n+1)+(n+1)Sn(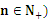 ,则与过点P(n,an)和点Q(n+2,an+1) (
,则与过点P(n,an)和点Q(n+2,an+1) (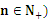 的直线平行的向量可以是 ( )
的直线平行的向量可以是 ( )| A.(1 , 2) | B.( , 2) , 2) | C.(2 ,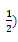 | D.(4 , 1) |
| A、10×211 | B、10×210 | C、11×211 | D、11×210 |
| lnnx | ||
|
| A、1 | B、2 | C、3 | D、4 |
一.选择
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
B
A
C
A
D
B
C
B
A
B
二.填空
13.
 14. 0
15.100 16. ②③④
14. 0
15.100 16. ②③④
三。解答题
17.(满分10分)
(1)

 ,∴
,∴ ,∴
,∴
 (5分)
(5分)
(2)

 ,∴f(x)的值域为
,∴f(x)的值域为 (10分)
(10分)
18.解:(1)拿每个球的概率均为 ,两球标号的和是3的倍数有下列4种情况:
,两球标号的和是3的倍数有下列4种情况:
(1,2),(1,5),(2,4),(3,6)每种情况的概率为:
所以所求概率为:
 (6分)
(6分)
(2)设拿出球的号码是3的倍数的为事件A,则 ,
, ,拿4次至少得2分包括2分和4分两种情况。
,拿4次至少得2分包括2分和4分两种情况。
 ,
, ,
, (12分)
(12分)
19 (满分12分)
解法一:(Ⅰ)取BC中点O,连结AO.

 为正三角形,
为正三角形, .……3分
.……3分
连结 ,在正方形
,在正方形
 中,
中, 分别为
分别为 的中点,
的中点,
由正方形性质知 ,
, .………5分
.………5分
又在正方形 中,
中, ,
,
 平面
平面 .……6分
.……6分
(Ⅱ)设AB1与A1B交于点 ,在平面
,在平面 1BD中,
1BD中,
作 于
于 ,连结
,连结 ,由(Ⅰ)得
,由(Ⅰ)得 .
.
 为二面角
为二面角 的平面角.………9分
的平面角.………9分
在 中,由等面积法可求得
中,由等面积法可求得 ,………10分
,………10分
又 ,
, .
.
所以二面角 的大小为
的大小为 .……12分
.……12分
 解法二:(Ⅰ)取
解法二:(Ⅰ)取 中点
中点 ,连结
,连结 .取
.取 中点
中点 ,以
,以 为原点,如图建立空间直角坐标系
为原点,如图建立空间直角坐标系 ,则
,则
 ……3分
……3分

 ,
, .
.
 平面
平面 .………6分
.………6分
(Ⅱ)设平面 的法向量为
的法向量为 .
. .
.


令 得
得 为平面
为平面 的一个法向量.……9分
的一个法向量.……9分
由(Ⅰ) 为平面
为平面 的法向量.……10分
的法向量.……10分
 .
.
 所以二面角
所以二面角 的大小为
的大小为 .……12分
.……12分
20.(满分12分)解:(I) ,
,
 ①
…2分
①
…2分
 ,
,
又

即 , ②
…4分
, ②
…4分
 ③
… 6分
③
… 6分
联立方程①②③,解得 … 7分
… 7分
(II)
 … 9分
… 9分
令
x
(-∞,-3)
-3
(-3,1)
1
(1,+∞)
f′(x)
+
0
-
0
+
f(x)

极大

极小

故h(x)的单调增区间为(-∞,-3),(1,+∞),单调减区间为(-3,1)
21.(满分12分)
解:(1)∵ ,∴
,∴ .
.
∴ (
( ).
).
∴ (
( ).
).
∴ (
( ).
).
∴ (
( ).
…3分
).
…3分
∴ 数列
数列 等比,公比
等比,公比 ,首项
,首项 ,
,
而 ,且
,且 ,∴
,∴ .
.
∴ .
.
∴ .
…6分
.
…6分
(2)


 .
.
 , ①
, ①
∴2
 . ②
. ②
①-②得 -
 ,
,

 ,
…9分
,
…9分
∴
 .
…12分
.
…12分
22.(满分12分)
A(0,b)知
 …2分
…2分
设 ,得
,得 …4分
…4分
因为点P在椭圆上,所以 …6分
…6分
整理得2b2= ,故椭圆的离心率e=
,故椭圆的离心率e= …8分
…8分
⑵由⑴知 ,
,
于是F(- a,0), Q
a,0), Q
△AQF的外接圆圆心为( a,0),半径r=
a,0),半径r= |FQ|=a
…10分
|FQ|=a
…10分
所以 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b= ,所求椭圆方程为
,所求椭圆方程为 …12分
…12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com