
题目列表(包括答案和解析)
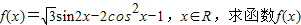 的最小正周期;
的最小正周期; ,若向量n=(1,sinA)与向量n=(2,sinB)共线,求a,b的值.
,若向量n=(1,sinA)与向量n=(2,sinB)共线,求a,b的值.| 1 |
| x |
|
|
 (t为参数),
(t为参数), (θ为参数).
(θ为参数). 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;已知函数
(I)若 满足
满足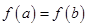 ,求
,求 的取值范围;
的取值范围;
(II)是否存在正实数 ,使得集合
,使得集合 ,如果存在,请求出
,如果存在,请求出 的取值范围;反之,请说明理由.
的取值范围;反之,请说明理由.
| 1 |
| an |
| 1 |
| an |
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
B
C
A
B
D
A
D
B
A
C
D
C
1、B
解: -
- =
= ,
, -
- =
= ,
, <
< ,故(A)错。
,故(A)错。
( +
+ )2=8+2
)2=8+2 ,(
,( +
+ )2=8+2
)2=8+2 ,故(B)对。
,故(B)对。
( +
+ )2=20+
)2=20+ ,(3+
,(3+ )2=20+
)2=20+ ,故(C)错。
,故(C)错。
5+ <5+
<5+ =8,故(D)也错。
=8,故(D)也错。
2、C
解:由 ,得
,得 ,即,-2<x-1<1,即-1<x<2,又x
,即,-2<x-1<1,即-1<x<2,又x Z,所以x为0,1,即N={0,1},故可选(C)。
Z,所以x为0,1,即N={0,1},故可选(C)。
3、A
解: =-
=- -2<0,故①错;
-2<0,故①错;
 =
= ≥0,故②对;
≥0,故②对;
 =
= ,因为
,因为 ,b符号不确定,故③不一定成立。
,b符号不确定,故③不一定成立。
对于④,因为a,b的符号不确定,也不成立。
4、B
解:当a,b都大于0时,由 ,得a≥b,所以,有
,得a≥b,所以,有 成立,
成立,
当a,b都小于0时,由 ,得a≤b,所以,有
,得a≤b,所以,有 成立,必要性成立。
成立,必要性成立。
而当a<b,且b<0时, 成立,
成立, 不成立,充分性不成立。
不成立,充分性不成立。
5、D
解:当x=0时,原不等式为 +4≥0显然成立,当x=2时,原不等式为
+4≥0显然成立,当x=2时,原不等式为 +4≥2
+4≥2 +2,即
+2,即 -2
-2 +2≥0,即(k2-1)2+1≥0,也成立,故选(D)。
+2≥0,即(k2-1)2+1≥0,也成立,故选(D)。
6、A
解:由x(3-x)>0,得x2-3x<0,解得:0<x<3。
7、D
解:由 ,且
,且 ,∴
,∴ ,∴
,∴
 。
。
8、B
解:依题意,有 ,解得:
,解得: ,f(x)=
,f(x)= ,
,
f(-x)= ,开口向下,与x轴交点为2,-1,对称轴为x=
,开口向下,与x轴交点为2,-1,对称轴为x=
9、A
解:依题意,直线经过圆的圆心,圆心为(-1,2),故有-2a-2b+2=0,即a+b=1,

 =
= =
= ≥
≥ =4
=4
10、C
解:如图知区域的面积是△OAB去掉一个小直角三角形。
(阴影部分面积比1大,比 小,故选C,不需要算出来)
小,故选C,不需要算出来)
11、D.由题意知直线 与圆
与圆 有交点,则
有交点,则 .
.
另解:设向量 ,由题意知
,由题意知
由 可得
可得
12、C
解:由 ,可得:
,可得:
知满足事件A的区域:的面积 10,而满足所有条件的区域
10,而满足所有条件的区域 的面积:
的面积: ,从而,得:
,从而,得: 。
。
二、填空题
13、
解:A= ,B=
,B= ,可求
,可求 。
。
14、3
 解:由
解:由 得
得 ,代入
,代入 得
得 ,当且仅当
,当且仅当 =3
=3 时取“=”.
时取“=”.
15、5
解:如图,由图象可知目标函数 过点
过点 时
时
 取得最大值,
取得最大值, ,
,
16、a≤0.
解:a≤ 在[1,2]上恒成立,a≤(
在[1,2]上恒成立,a≤( )min=(
)min=( )min=0.
)min=0.
三、解答题
17、解:(I)由 ,得
,得 .
.
(II) .
.
由 ,得
,得 ,又
,又 ,所以
,所以 ,
,
即 的取值范围是
的取值范围是 .
.
18.解:(Ⅰ)由题意得:


(Ⅱ)设框架用料长度为 ,
,
则


当且仅当
 满足
满足
答:当  米,
米, 米时,用料最少.
米时,用料最少.
19、解:(1)依题意三角形NDC与三角形NAM相似,
所以 ,即
,即 ,
,  ,
,
矩形ABCD的面积为 ,定义域为
,定义域为 ,
,
要使仓库占地ABCD的面积不少于144平方米即 ,
,
化简得 ,解得
,解得 所以AB长度应在
所以AB长度应在 内.
内.
(2)仓库体积为
 得
得 ,
,
当 时
时 ,当
,当 时
时 所以
所以 时V取最大值
时V取最大值 米3,
米3,
即AB长度为20米时仓库的库容最大.
20、解:(1)
即 (
( );
);
(2)由均值不等式得:
 (万元)
(万元)
当且仅当 ,即
,即 时取到等号.
时取到等号.
答:该企业10年后需要重新更换新设备.
21、设
 ,
,


 =
=
因为 是
是 的必要不充分条件,所以
的必要不充分条件,所以

 ,且
,且 推不出
推不出
而 ,
,
所以 ,则
,则
即
22、解:设
连结BD.
则在 中,
中,


设
则
等号成立时
答:当 时,建造这个支架的成本最低.
时,建造这个支架的成本最低.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com