
题目列表(包括答案和解析)
(14分)已知抛物线、椭圆、双曲线都经过点M(1,2),它们在x轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求这三条曲线方程;
(Ⅱ)若定点P(3,0),A为抛物线上任意一点,是否存在垂直于x轴的直线l被以AP为直径的圆截得的弦长为定值?若存在,求出l的方程;若不存在,说明理由。(14分)设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1,在满足条件①、②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程。
、(本小题满分14分)
已知函数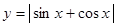
(1)画出函数在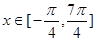 的简图;
的简图;
(2)写出函数的最小正周期和单调递增区间;并求:当x为何值时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状。
14分)已知椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1),且其右焦点到直线x-y+ =0的距离为3.(I)求椭圆的方程;
=0的距离为3.(I)求椭圆的方程;
(II)是否存在斜率为k(k≠0)的直线l,使l与已知椭圆交于不同的两点M、N,
且|AN|=|AM|?若存在,求出k的取值范围;若不存在,请说明理由.
一、选择题
1-5BCABC 6-10ABDBC 11-12DB
二、填空题
13、等腰14、  15、
15、 16、
16、
三、解答题
17、解:设三数为
 或
或
则三数为

 或
或
 ,
,
18、解: 16.解:当a=0时,不等式的解为x>1;当a≠0时,分解因式a(x- )(x-1)<0
)(x-1)<0
当a<0时,原不等式等价于(x- )(x-1)>0,不等式的解为x>1或x<
)(x-1)>0,不等式的解为x>1或x< ;
;
当0<a<1时,1< ,不等式的解为1<x<
,不等式的解为1<x< ;
;
|