
题目列表(包括答案和解析)
甲、乙两个同学做数学游戏,规则是:甲先报一个不为零的数,乙就说出甲所说数的两倍小1的数,接着甲说出比乙所说数小1的数,乙又说出甲第二次所说数的2倍,如此下去,先报0者为胜.若你是甲,为了取胜,你应报怎么样的数?请至少举出四![]() 个数.
个数.
 假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话:
假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话:| 2 |
| 3 |
 )
)
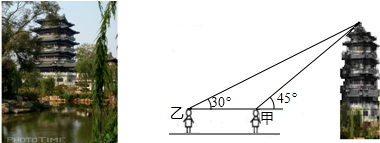 假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话:
假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话: )
)| 颜色 | 蓝 | 红 | 紫 |
| 次数 | 202 | 600 |


一、选择题
1. B; 2. B; 3. B; 4. C; 5. A; 6. C.
二、填空题
7. x≥―1且x≠2; 8. 9; 9. 97; 10. 答案不唯一,如 等;
等;
11. 略; 12.  ; 13. 6,150; 14.
4; 15.
; 13. 6,150; 14.
4; 15.  .
.
三、解答题
16.原式=  ------------------------------4分
------------------------------4分
=  -- --------------------------------------------------------------6分
-- --------------------------------------------------------------6分
=  .-----------------------------------------------------------------------------7分
.-----------------------------------------------------------------------------7分
17.(1) 证明:在 中,
中, --2分
--2分
∵ 分别是
分别是 的中点,∴
的中点,∴ . ∴
. ∴ .---------4分
.---------4分
(2) 四边形 是矩形.
是矩形.
证明:∵四边形 是菱形,∴
是菱形,∴ . ----------------5分
. ----------------5分
∴ . -----------------------------------------------------------------------6分
. -----------------------------------------------------------------------6分
∵ ∴四边形
∴四边形 是平行四边形. -------------
7分
是平行四边形. -------------
7分
∴四边形 是矩形. -------------------------------------------------------------
8分
是矩形. -------------------------------------------------------------
8分
18.解:过 作
作 ,垂足为
,垂足为 , ----------------------------------------1分
, ----------------------------------------1分
在 中,
中, ∴
∴ ----------------------3分
----------------------3分
在 中,
中,  ,∴
,∴  ------------------5分
------------------5分
∴ ------------------------------------6分
------------------------------------6分
 --------------------8分
--------------------8分
19.(1)证明:在等腰梯形 中,
中, ,
,
∴ --------------------------------------------------1分
--------------------------------------------------1分
∵ ,
, ,
,
∴ ∴
∴ .
-------------3分
.
-------------3分
(2) 解:过 分别作
分别作 ,垂足分别为
,垂足分别为 .
.
∴ --------------------------------------------------------------------5分
--------------------------------------------------------------------5分
∵ , ∴
, ∴ ----------------------------------------------6分
----------------------------------------------6分
∵ ,∴
,∴ ------------------------------------------------------7分
------------------------------------------------------7分
(2) 解:存在.
由(1)知 .∴
.∴ . -----------------------------------------8分
. -----------------------------------------8分
∵ ,∴
,∴ .
---------------------------------------9分
.
---------------------------------------9分
解得: 或
或 --------------------------------------------------------10分
--------------------------------------------------------10分
20.解:(1)原来一天可获得的利润为 (元)-------2分
(元)-------2分
(2). ① 由题意,得 .
.
即 .
------------------4分
.
------------------4分
 .
----------------------------------------------- 5分
.
----------------------------------------------- 5分
② 当 时,
时, . ----------------------------6分
. ----------------------------6分
解这个方程,得 . ----------------------------------------------------------------8分
. ----------------------------------------------------------------8分
答:出售单价是77元或73元. ----------------------------------------------------------------9分
 73元
73元 77元.
----------------------- 10分
77元.
----------------------- 10分
21.解:(1)列表格如下:
( )
)

1
2
3
4
5
6

1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
----------------------------------------5分
⑵由函数解析式 可知:只有点(1,4)和(3,1)在其图像上,所以,甲获胜的概率是
可知:只有点(1,4)和(3,1)在其图像上,所以,甲获胜的概率是 ,即平均每12次才获胜1次,得10分;而乙获胜的概率是
,即平均每12次才获胜1次,得10分;而乙获胜的概率是 ,即平均每12次获胜11次,得11分,所以我愿意当乙.--------------------- 10分
,即平均每12次获胜11次,得11分,所以我愿意当乙.--------------------- 10分
22.(1) 四边形 是平行四边形. ------------------------------1分
是平行四边形. ------------------------------1分
证明:
 .又
.又 ,
, .
. 又
又
 .
.
 四边形
四边形 是平行四边形. -----------------------------------4分
是平行四边形. -----------------------------------4分
(2)  是
是 的重心,
的重心, . ---------------------------5分
. ---------------------------5分
由(1)的证明过程,可知 和
和 分别是边长为
分别是边长为 和
和 的正三角形.
的正三角形.
 点
点 到
到 的距离为
的距离为 .即
.即 .
. -----------------8分
-----------------8分 ,
, 时, 四边形
时, 四边形 的面积
的面积 有最大值是
有最大值是 .
.
此时, 与
与 重合,
重合, , 四边形
, 四边形 是菱形. -------------------------11分
是菱形. -------------------------11分
23.解:⑴过点 作
作 轴,垂足为
轴,垂足为 ,由垂径定理,得
,由垂径定理,得 是
是 的中点,
的中点,
 .
. 与
与 轴相切于
轴相切于 在
在 中,
中,

 点
点 的坐标是
的坐标是 .
-----------------2分
.
-----------------2分
设 的解析式为
的解析式为 .将
.将 两点的坐标代入,得
两点的坐标代入,得 解得
解得
 所在直线的解析式为
所在直线的解析式为 --------------------- 4分
--------------------- 4分
(2) ∵ ,∴
,∴ 连结
连结 .
.
∵ ,∴
,∴ -----------------------6分
-----------------------6分
∴ ∵
∵ 是直径,∴
是直径,∴
∴ -------------------------------------------------------------------8分
-------------------------------------------------------------------8分
(3) 判断:不存在. ----------------------------------------------------------------- 9分
假设存在点 ,使
,使 为等边三角形.则
为等边三角形.则 .连结
.连结 ,那么
,那么 .
. ,利用
,利用 的面积,可得
的面积,可得 ,
, 不与
不与 重合,
重合,  .这与等边三角形定义矛盾.
.这与等边三角形定义矛盾.
 假设不成立.即点
假设不成立.即点 不存在. ----------------------------------------------------------- 12分-
不存在. ----------------------------------------------------------- 12分-
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com