
题目列表(包括答案和解析)
| CB |
| AC |
| AC |
| AB |
| ||
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BC |
| AC |
| BC |
| B1C1 |
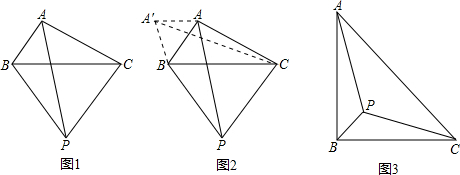
| 2 |
| 6 |
32+16
|
| 2 |
| 6 |
32+16
|
一、BCACB CBADD
二、11. a4 12. (1)
17. 如果AB=AD,BC=DC,那么∠ACB=∠ACD(或如果∠ACB=∠ACD,BC=DC,那么AB=AD)
18. 2
三、19.(1)原式 ………………………………(3分)
………………………………(3分)
 ………………………………(4分)
………………………………(4分)
 ………………………………(5分)
………………………………(5分)
当 时,原式
时,原式 ………………………………(8分)
………………………………(8分)
20.(1)方程两边都乘以(x+1)(x-1),约去分母,得 x-1=-2 …………(2分)
解这个整式方程,得 x=-1 ………………………………(4分)
检验: 把x=-1代入(x+1)(x-1),得(x+1)(x-1)=0,
因此,x=-1不是原分式方程的根,所以原分式方程无解. ………(5分)
(2)原方程整理,得 x2-2x=2 …………………………(1分)
(x-1)2=3 …………………………(3分)
x-1=± …………………………(4分)
…………………………(4分)
∴ x1=1+ , x2=1-
, x2=1- …………………………(5分)
…………………………(5分)
21.(1)这8天该类饮料平均日销售量是
 (2×31+2×33+29+32+25+26)=30(箱) …………………………(4分)
(2×31+2×33+29+32+25+26)=30(箱) …………………………(4分)
(2)估计上半年该店能销售这类饮料181×30=5430(箱) …………(8分)
22.设原价为1个单位,每次提价的百分率为x. ………………………(1分)
根据题意,得
(1+x)2= ………………………………(4分)
………………………………(4分)
解这个方程,得 (舍去) ………………(6分)
(舍去) ………………(6分)
取 .
………………………………(7分)
.
………………………………(7分)
答:每次提价的百分率约为22.5%. ………………………………(8分)
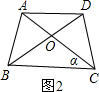
23. 证明:∵ OA=OB,
∴ ∠A=∠B. ……………………………(3分)
又 ∵ AC=BD,
∴ △OAC≌△OBD, ………………………………(7分)
∴ OC=OD, ………………………………(9分)
∴ ∠1=∠2. ………………………………(10分)
注:本题证法不唯一,其它证法可参照上述步骤给分.
24.(1)∵ 四边形ABCD和DCEF都是正方形,
∴ CD=DF,∠DCG=∠DFH=∠FDC=90°. ……………………………(2分)
∵ ∠CDG+∠CDH=∠CDH+∠FDH=90°,
∴ ∠CDG=∠FDH, ………………………………(4分)
∴ △CDG≌△FDH, ………………………………(5分)
∴ CG=FH. ………………………………(6分)
∵ BC=EF,
∴ BG=EH. ………………………………(8分)
(2)结论BG=EH仍然成立. ………………………………(9分)
同理可证△CDG≌△FDH. ………………………………(10分)
∴ CG=FH,
∵ BC=EF,
∴ BG=EH. ………………………………(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com