练习册

  • 练习册
  • 试题
    (1)在递增数列中.与是关于的方程(为正整数)的两个根．求的通项公式并证明是等差数列, 【查看更多】

     

    题目列表(包括答案和解析)

     （08年扬州中学） （16分）

    用表示数列从第项到第项（共项）之和．

    （1）在递增数列中，与是关于的方程（为正整数）的两个根．求的通项公式并证明是等差数列；

    （2）对（1）中的数列，判断数列，，，…，的类型；

    （3）对一般的首项为，公差为的等差数列，提出与（2）类似的问题，你可以得到怎样的结论，证明你的结论．

     

    查看答案和解析>>

    如图1-14,在正方形ABCD中，E是BC的中点，F是CD上一点,AE⊥EF,则下列结论正确的是(    )

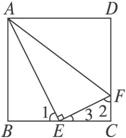
    图1-14

    A.∠BAE=30°         B.CE2=AB·CF       C.CF=CD          D.△ABE∽△AEF

    查看答案和解析>>

    （1）在演绎推理中，只要     是正确的，结论必定是正确的．
    （2）用演绎法证明y=x2是增函数时的大前提是     ．
    （3）由“等腰三角形的两腰相等”可以类比推出正棱锥的类似属性是     ．

    查看答案和解析>>

    （1）在演绎推理中，只要 ______是正确的，结论必定是正确的．
    （2）用演绎法证明y=x2是增函数时的大前提是 ______．
    （3）由“等腰三角形的两腰相等”可以类比推出正棱锥的类似属性是 ______．

    查看答案和解析>>

    （1）在演绎推理中，只要     是正确的，结论必定是正确的．
    （2）用演绎法证明y=x2是增函数时的大前提是     ．
    （3）由“等腰三角形的两腰相等”可以类比推出正棱锥的类似属性是     ．

    查看答案和解析>>


    同步练习册答案