
题目列表(包括答案和解析)
(本小题满分15分)某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限 | 3 | 5 | 6 | 7 | 9 |
| 推销金额 | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)求年推销金额![]() 与工作年限x之间的相关系数;(Ⅱ)求年推销金额
与工作年限x之间的相关系数;(Ⅱ)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.(参考数据:;由检验水平0.01及
的线性回归方程;(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.(参考数据:;由检验水平0.01及![]() ,查表得
,查表得![]() .)
.)
(本小题满分15分) 如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,
的中点,![]() 底面
底面![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)当![]() 为何值时,
为何值时,![]() 在平面
在平面![]() 内的射影恰好为
内的射影恰好为![]() 的重心.
的重心.
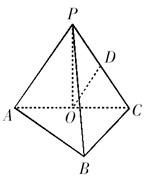
(本小题满分15分)
已知向量 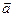 =(cos
=(cos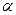 ,sin
,sin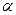 ),
),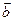 =(cos
=(cos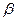 ,sin
,sin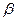 ),|
),|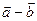 |=
|=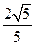 .
.
(1)求cos(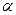 -
-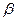 )的值;
)的值;
(2)若0<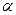 <
<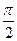 ,-
,-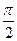 <
<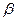 <0,且sin
<0,且sin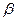 =-
=-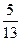 ,求sin
,求sin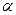 的值
的值
(本小题满分15分)
设函数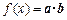 ,其中向量
,其中向量 ,
, ,
,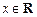 ,且
,且 的图象经过点
的图象经过点 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数 的最小值及此时
的最小值及此时 值的集合.
值的集合.
(本小题满分15分)已知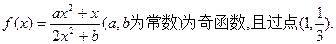
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)定义正数数列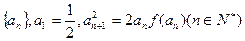 ,证明:数列
,证明:数列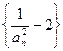 是等比数列;
是等比数列;
|
 成立的最小n值.命题人:袁卫刚 校对人:沈秋华
成立的最小n值.命题人:袁卫刚 校对人:沈秋华一.选择题(5分×10)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
A
C
B
C
C
D
A
C
二.填空题(5分×6)
11. 12.
12. 13、 2400 14.
13、 2400 14.  15.
15.  16、
16、
三.解答题
17.(12分)
解:(1)由 ,得
,得
由 ,知
,知 ……………………………………4/
……………………………………4/
解得, ……………………………………6/
……………………………………6/
(2)若 时,不等式的解集为A=
时,不等式的解集为A= ;
;
若 时,不等式的解集为A=
时,不等式的解集为A= ……………… 12/
……………… 12/
18(14分)
解:(1) ,
, ………………2/
………………2/
 ,而
,而 ,符合上式
,符合上式
 ……………………………………8/
……………………………………8/
(2)由
 ……………………………………10/
……………………………………10/
 T4+T15=149 ……………14/
T4+T15=149 ……………14/
19(14分)
解:(1)a,b,c依次成等差数列,得2b=a+c
又 ,
, ………………………………3/
………………………………3/
设 ,则
,则 最大角为C
最大角为C
由 ,得
,得 ………………………………6/
………………………………6/
(2)由 b=1,a+c=2 ………………………………7/
又由 得
得

 ………………………………10/
………………………………10/
 从而△ABC的面积为
从而△ABC的面积为 ………………………………14/
………………………………14/
20.(15分)
解:(1)由题意, ,显然q≠1 ………………………………2/
,显然q≠1 ………………………………2/
 ,解得
,解得 ………………………5/
………………………5/
由 ,
,

 成等差数列
………………………8/
成等差数列
………………………8/
(2) …………………10/
…………………10/


两式相减,得

 =
=
 …………………………………………15/
…………………………………………15/
21.(15分)
解:由题设知,每年的经费是以12为首项,4为公差的等差数列
设纯利润与年数的关系为 ,
,
则
(I)获纯利润就是要求 ,
,
即 ,
,
 ,
,
 从第3年开始获利.
…………………………………………6/
从第3年开始获利.
…………………………………………6/
(II)(1)年平均纯利润 ,
,
 ,当且仅当
,当且仅当 时,取“=”号,
时,取“=”号,
 ,
,
 第(1)种方案共获利
第(1)种方案共获利 (万元),此时
(万元),此时 . …………10/
. …………10/
(2) ,
,
当 时,
时, .
.
故第(2)种方案共获利 (万元).
…………13/
(万元).
…………13/
比较两种方案,获利都为144万元,但第(1)种方案需6年,而第(2)种方案需10年,故选择第(1)种方案. ……………………15/




 2005――2006学年(下)期中联考
2005――2006学年(下)期中联考
高 一 数 学 (A卷)
题 号
二
三
总分
17
18
19
20
21
得 分
评卷人
二.填空题(本大题共6小题,每小题5分,共30分)
11. ;
12. ;
13. ;
14. ;
15. ;
16. .
三.解答题:
17.(14分)
18. (14分)
19. (14分)
20. (14分)
21. (14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com